Time Series Forecasting: Regression oder ARIMA Models?

Die Vorhersage von Zeitreihen ist eine wichtige statistische Methode zur Schätzung zukünftiger Trends. Im Rahmen des Time Series Forecastings lassen sich zahlreiche Modelle identifizieren, die sich für die Prognose von Zeitreihen heranziehen lassen. Zwei bekannte Formen bilden hierbei die Regressions- und ARIMA-Modelle (AutoRegressive Integrated Moving Average). Dieser Beitrag soll Ihnen helfen, die Unterschiede dieser Modelltypen zu verstehen, und eine Entscheidungshilfe bei der Wahl des passenden Modells bieten.

Sie suchen anspruchsvolle Lösungen mit Blick auf die Erstellung von Time Series Forecasts mit ARIMA- oder Regressionsmodellen? Gerne unterstützen unsere Expert*innen Sie in Form eines persönlichen Coachings. Kontaktieren Sie uns noch heute für eine professionelle Statistik Beratung!

Was genau ist Time Series Forecasting?

Das Hauptziel der Zeitreihenanalyse (oder Time Series Forecasting im Englischen) besteht in der Konstruktion mathematischer Modelle. Diese sollen eine nachvollziehbare Darstelung erhobener Stichproben-Daten liefern. Da zeitbasierte Datensätze scheinbar zufällig über die Zeit hinweg schwanken, ist es wichtig, diese adäquat beschreiben und anschließend statistisch modellieren zu können. Hierfür werden die erfassten Merkmale als eine Ansammlung von Zufallsvariablen definiert. Entlang ihres zeitlichen Auftretens erfolgt dann eine Indizierung mit Blick auf die zeitliche Achse.

So können wir eine Zeitreihe als eine Sequenz von Zufallsvariablen, x₁, x₂, x₃, …, x_n betrachten. Die Zufallsvariable x₁ bezeichnet dabei den Wert, den die Reihe zum ersten Zeitpunkt annimmt. Die Variable x₂ repräsentiert den Wert am zweiten Punkt der Messung, x₃ den Wert am dritten Punkt der Messung und so weiter. Ganz allgemein wird eine Sammlung von Zufallsvariablen x_t, die nach t indiziert sind, als ‘stochastischer Prozess’ betrachtet. In der nachstehenden Abbildung findet sich exemplarisch eine Zeitreihe des Aktienkurses der Apple Aktie (AAPL).

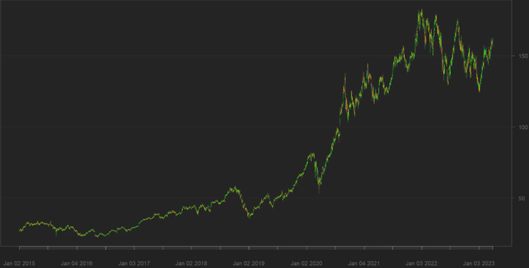
Time Series Forcasting in der Praxis

Basierend auf der Datenerhebung lassen sich verschiedene Gründe anführen, weshalb eine komplexe statistische Modellierung erfolgen sollte. Im vorliegenden Beispiel des Aktienkurses wäre es denkbar, dass Investoren auf Basis vorhergehender Kursverläufe Prognosen über bevorstehende Entwicklungen treffen wollen. So könnten sie ihre Aktienbestände anpassen, um maximale Renditen zu erreichen. Aber auch volkswirtschaftliche Trends lassen sich aus den Kursverläufen ableiten. Diese sind für Entscheidungsträger mit wirtschaftspolitischer Verantwortung von großer Bedeutung, da sich Entscheidungen an empirisch messbaren Veränderungen orientieren können.

Auch die Planung und strategische Ausrichtung von Unternehmen, Behörden oder vergleichbarer Einheiten lässt sich an Zeitreihenanalysen und damit verbundenen Prognosen ausrichten. Szenarien, in denen ein solches Vorgehen erfolgen kann, gestalten sich vielfältig. Denkbar sind z. B. Wettermodelle, Risikoanalysen von Vermögensverwaltungen oder die Planung von Verkehrsströmen. Die Anwendung im Rahmen von Umsatzanalysen und Kostenanalysen ist ebenfalls sehr geläufig.

Regression als Time Series Forecasting Methode

Lineare Regressionsmodelle werden häufig zur Prognose zukünftiger Werte in Zeitreihen genutzt. Sie beruht auf der Annahme, dass eine lineare Beziehung zwischen einer abhängigen Variable und einer oder mehreren unabhängigen Variablen besteht. Im Time Series Forecasting kann die lineare Regression beispielsweise dabei helfen, den Zusammenhang zwischen einer spezifischen abhängigen Variable (z. B. dem Kursverlauf von Aktien) und einer oder mehrerer weiterer Variablen (z.B. Inflation, Lohnentwicklung) zu modellieren. Mithilfe dieser Beziehung lässt sich eine Prognose für zukünftige Werte der abhängigen Variablen erstellen.

Wichtig ist in diesem Fall, dass die Vorhersage auf Grundlage zusätzlicher Variablen erfolgt, die neben der interessierenden abhängigen Variable erhoben werden müssen. Dazu werden historische Daten genutzt, um eine lineare Gleichung zu erstellen, die den Zusammenhang zwischen den Variablen beschreibt. Anschließend besteht die Möglichkeit, diese Gleichung zur Prognose zukünftiger Werte der abhängigen Variablen zu verwenden. 

ARIMA als Time Series Forecasting-Methode

ARIMA kann als Prognosemodellierung für Zeitreihen dienen, die im Gegensatz zur linearen Regression auch Trends und saisonale Effekte in Betracht zieht. Ein traditionelles ARIMA-Modell besteht aus drei Komponenten:

• einer autoregressiven Komponente,
• einer integrierten Komponente und
• einer gleitenden Durchschnittskomponente

Die autoregressive Komponente gründet auf der Annahme, dass der aktuelle Wert einer Zeitreihe von vorherigen Werten abhängt. Mittels der integrierten Komponente kann man eine nicht-stationäre Zeitreihe in eine stationäre transformieren, indem Differenzen aufeinanderfolgender Messwerte gebildet werden. Dieser Schritt ist notwendig, um ARIMA-Modellierungen zu vollziehen. Die gleitende Durchschnittskomponente modelliert wiederum aktuelle Werte auf Grundlage zufälliger Schwankungen.

Die Erstellung von ARIMA-Modellen und den beschriebenen Komponenten erfolgt anhand von Schätzungen historischer Daten. Mit diesen lassen sich anschließend künftige Werte der Zeitreihe prognostizieren. Dabei können sowohl kurz- als auch langfristige Trends und saisonale Effekte in die Modellierung einfließen. Die Anwendung von ARIMA-Modellen gilt allgemein als anspruchsvoll und erfordert ein ausreichendes Maß an Erfahrung in der Modellierung von Zeitreihen.

Fazit

Time Series Forecasting ist ein nützliches Verfahren zur Vorhersage zukünftiger Werte von Variablen ist, die über einen spezifischen Zeitraum hinweg erhoben wurden. Das Ziel besteht darin, auf der Grundlage vergangener Werte sowie möglicher weiterer Faktoren zukünftige Werte der Variablen zu prognostizieren.

Bei weiteren Fragen zur Durchführung und Interpretation einer Zeitreihenanalyse mittels Time Series Forecasting freuen wir uns über Ihre unverbindliche Kontaktaufnahme. Gerne erstellen wir Ihnen umgehend ein unverbindliches Angebot. 

Nutzen Sie dazu gleich und unverbindlich unser schriftliches Kontaktformular.

Weiterführende Links

Juan Nathaniel: Introduction to ARIMA for Time Series Forecasting. 2021. https://medium.com/m/global-identity-2?redirectUrl=https%3A%2F%2Ftowardsdatascience.com%2Fintroduction-to-arima-for-time-series-forecasting-ee0bc285807a

Klaus Backhaus et al. Zeitreihenanalyse. In: Multivariate Analysemethoden. Springer Gabler, Berlin, Heidelberg. 2018. https://link.springer.com/chapter/10.1007/978-3-662-56655-8_3