Eine deskriptive Statistik beschreibt einen Datensatz und deren Eigenschaften. Das Ziel der deskriptiven (beschreibenden) Statistik ist es meist, eine Stichprobe von empirischen Daten zu beschreiben.
Die deskriptive Statistik verwendet Kennzahlen für die Häufigkeiten der Werte, die Lage der Daten (wie den Mittelwert), deren Verteilungsbreite (z.B. Standardabweichung) und Symmetrie dieser Verteilung, Tabellen oder Grafiken, oder mehrere davon.
Sollten Sie Unterstützung bei der Erhebung oder Analyse empirischer Daten benötigen, helfen unsere Statistiker Ihnen gerne weiter. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Gründe für die deskriptive Statistik
Aufgrund der deskriptiven Beschreibung einer Stichprobe lässt sich beurteilen, ob die Stichprobe repräsentativ sein könnte für eine grössere Grundgesamtheit, z.B. wenn sie dieselben Eigenschaften besitzt. Umgekehrt sind die Daten sicher nicht repräsentativ, wenn die Stichprobe sich von der Gesamtbevölkerung deutlich unterscheidet. Hat man beispielsweise nur Männer befragt, gelten die Ergebnisse nicht für alle Menschen. Man kann dann eventuell mit Hilfe induktiver Verfahren (Inferenzstatistik) auf die Meinung der Frauen schliessen.
Eine deskriptive Beschreibung der Daten gehört zu jeder vollständigen statistischen Datenauswertung und -darstellung dazu, ist aber meist nicht der Endzweck, sondern nur der Anfang der Auswertung.
Häufigkeiten der Werte
Die erste Kennzahl für eine deskriptive Statistik ist die Anzahl n der Datensätze oder Versuchspersonen / Teilnehmer/innen.
Jeder Datensatz enthält mehrere Variablen, die wiederum mehrere Werte annehmen können. Es interessiert nun auch, wie häufig welcher der möglichen Werte gemessen bzw. beobachtet wurde. Hierbei unterscheidet man zwischen der absoluten und der relativen Häufigkeit. Die absolute Häufigkeit gibt die Anzahl an, d.h. in wie vielen Datensätzen dieser Wert auftrat. Die Summe aller absoluten Häufigkeiten ergibt die Anzahl der Datensätze.
Die relative Häufigkeit eines Wertes errechnet sich aus der absoluten Häufigkeit, die man durch die Anzahl n der Datensätze teilt.
Lageparameter
Lageparameter der Datenverteilung messen, ob die Werte gross oder klein ausgefallen sind. Wurden z.B. eher ältere oder jüngere Menschen befragt?
- Mittelwert (arithmetisches Mittel): Den Mittelwert bzw. Durchschnitt berechnet man, indem man alle Werte aufsummiert und dann durch die Anzahl der Werte teilt. Diese Kenngrösse macht jedoch nur Sinn für Variablen, die mindestens intervallskaliert sind. Bei kleinen Stichproben ist der Mittelwert empfindlich gegenüber Ausreissern: Ein sehr grosser oder sehr kleiner Ausreisser-Wert kann den Mittelwert nach oben oder unten verzerren.
- Median: Der Median wird so gewählt, dass es bei einer geordneten Reihe von Messwerten genauso viele Werte darüber wie darunter gibt. Bei einer ungeraden Anzahl an Werten ist es genau der mittlere. Die Werte sollten mindestens ordinalskaliert sein.
- Modalwert bzw. Modus: Dabei handelt es sich um den Wert in einer Verteilung, der am häufigsten auftritt. Werden Werte zu Klassen zusammengefasst, gilt die Klassenmitte der häufigsten Klasse als Modalwert der Verteilung. Diese Grösse kann für alle Skalenniveaus verwendet werden, auch für eine Nominalskala. Sie ist robust gegenüber Ausreissern.
Verteilungs-Parameter
Die Verteilung beschreibt die Breite der Streuung oder Dispersion der Werte um den Mittelwert.
- Variationsbreite: Diese Spannweite der Daten misst den Abstand zwischen Minimal- und Maximal-Wert. Bei nominalskalierten Daten ist die Variationsbereite gleich der Anzahl der Kategorien. Allerdings hängt diese Grösse nur von den beiden extremsten Werten ab und macht keine Aussage über die Verteilung der Werte dazwischen.
- Quartile: Die Werte Q1, Q2 und Q3 teilen eine Verteilung in jeweils vier gleich grosse Abschnitte mit gleich vielen Datensätzen auf. Das mittlere Quartil entspricht dabei dem Median. Die Hälfte des Abstands zwischen Q3 und Q1 wird als mittlerer Quartilabstand bezeichnet. Quartile machen nur bei mindestens ordinalskalierten Werten Sinn.
- mittlere Abweichung: Man berechnet die mittlere Abweichung der Werte jeweils vom Mittelwert. Bei einer symmetrischen Verteilung ergibt dieser Wert null. Darum kann es auch Sinn machen, die mittlere absolute Abweichung zu berechnen, also den Mittelwert der absoluten Abweichungen der Werte vom Mittelwert.
- Standardabweichung: Die Stichproben-Varianz berechnet sich als Mittelwert der Abweichungsquadrate, d.h. als Summe der quadrierten Abstände der einzelnen Messwerte vom Mittelwert, die dann durch (n-1) geteilt wird. (n sei die Stichprobengrösse.) Die Standardabweichung berechnet sich als die Wurzel der Varianz. Die Daten müssen mindestens intervallskaliert sein.
- Variationskoeffizient: Der Variationskoeffizient teilt die Standardabweichung durch den Mittelwert. Der Variationskoeffizient erlaubt den Vergleich der Streuung von Stichproben mit unterschiedlichen Mittelwerten, wenn die Werte zu einer Verhältnisskala gehören.
Symmetrie-Parameter
Bei einer symmetrischen Verteilung der Daten fallen Mittelwert, Median und Modus auf denselben Wert. Bei einer rechtsschiefen Verteilung liegen Median und Modus links vom arithmetischen Mittelwert (und der Modus links vom Median). Bei einer linksschiefen Verteilung ist es genau umgekehrt. Die Schiefe v(x) lässt sich quantifizieren durch:
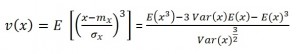
Hier sind x die empirischen Werte, m und sigma jeweils Mittelwert und Standardabweichung, E(x) und Var(x) Erwartungswert und Varianz. Linksschiefe Verteilungen haben v(x) < 0, rechtsschiefe v(x) > 0.
Tabellen
Eine deskriptive Beschreibung von Daten in einer Tabelle kann so aussehen: Sie enthält einen Datensatz (Beobachtung) pro Zeile und eine Variable pro Spalte. Zur besseren Übersichtlichkeit können die Daten zusammengefasst und aggregiert werden oder farblich markiert. Beispielsweise könnte man den Daten verschiedene Farben geben, abhängig davon, zu welchem Quantil sie gehören. Es können auch mehrere Variablen zu einer einzigen (einem Index) zusammengefasst werden oder durch Klassenbildung eine stetige in eine diskrete Variable umgewandelt werden, z.B. wenn man die Befragten nach Alter in Kohorten einteilt jeweils für ein Alter <20, 20-30, 30-40, 40-50 und >50 Jahre.
Eine deskriptive Tabelle kann auch die Häufigkeiten der einzelnen auftretenden Werte angeben.
Eine Kontingenztabelle stellt für die Kombinationen zweier Variablen deren Häufigkeiten dar. Dabei werden die Werte der einen Variablen als Bezeichnung der Spalten und der anderen für die Zeilen verwendet. In jedem Feld steht dann die absolute oder relative Häufigkeit, mit der die Wertekombination der beiden Variablen-Werte auftrat.
Grafiken
Anschaulicher als eine Tabelle sind Grafiken. Folgende drei Grafiken werden für deskriptive Statistiken am häufigsten verwendet:
Histogramm (Säulendiagramm) für die Darstellung der Häufigkeiten von Werten. Dabei wird jeder Wert durch eine senkrechte Säule dargestellt und deren Höhe ist proportional zur Häufigkeit des Wertes. Ein Balkendiagramm sieht ähnlich aus, nur dass hier die Balken waagrecht verlaufen statt senkrecht.
Kreisdiagramme (“Tortengrafik”) machen vor allem bei Nominalskalen Sinn. Der Anteil eines Segments an der Gesamtfläche wird üblicherweise proportional zur Häufigkeit gewählt.
Der Boxplot erfasst die wichtigsten Lage- und Streuparameter einer Verteilung grafisch. Er zeichnet für jeden Wert einen Kasten, der beim ersten Quantil Q1 beginnt und beim dritten Quantil Q3 endet. Somit ist die Länge der Box proportional zum Quartilabstand. Der Median wird durch einen Punkt oder eine durchgezogene Linie in der Box dargestellt. Zwei Linien ausserhalb der Box reichen bis an den Minimal- und Maximalwert heran.