In einem früheren Beitrag haben wir das Beispiel einer Medikamentenstudie präsentiert, in der bei vielen Einzelpersonen Messwerte zu unterschiedlichen Zeitpunkten erhoben wurden. Da sich Menschen auch in Aspekten unterscheiden, die nicht gemessen werden können, besteht bei solchen Studien immer das Problem der Autokorrelation. Das heisst, dass wir Messwerte in Stichproben als unabhängig betrachten, obwohl sich in diesen Werten eines einzigen Merkmals im Zeitverlauf ein (systematischer) Zusammenhang beobachten lässt, wir also genau genommen eine abhängige Stichprobe haben.
Die ANOVA mit Messwiederholungen gehört zu den bekanntesten Methoden, um eine solche abhängige Stichprobe zu bearbeiten. Wir stellen in diesem Beitrag eine alternative Anwendungsmöglichkeit basierend auf gemischten Modellen (mixed models) vor, die nützliche zusätzliche Funktionen bietet und vor allem bei der Verwendung von Erklärungsvariablen in Stichproben für übersichtlichere Ergebnisse sorgt.
Wir unterstützen Sie gerne bei der Aufstellung von gemischten Modellen und bei der Durchführung von Analysen mit Stichproben mittels SPSS. Wenden Sie sich hierfür gerne und unverbindlich an uns für eine professionelle Statistik Hilfe.
Kurz wiederholt: ANOVA mit Messwiederholung
Die Varianzanalyse (oder: ANOVA) basiert auf der Idee der Varianzzerlegung. In der Variante mit Messwiederholungen, sprich: wenn eine abhängige Stichprobe vorliegt, kann die Gesamtvarianz der Messwerte in zwei Komponenten zerlegt werden:
- Varianz innerhalb der Einzelwerte: Dies wird auch als geschätzter Zeiteffekt bzw. Behandlungseffekt bezeichnet.
- Varianz zwischen den Werten: Dabei handelt es sich um die geschätzte Differenz im Basisniveau, d.h. bestimmte Messwerte (zB. Bluthochdruck) können nicht null sein und liegen bereits zu Beginn der Untersuchung auf einem bestimmten Niveau.
Beide Komponenten werden um den Messfehler ergänzt. In einer Analyse ohne Drittvariablen sind wir lediglich an dem Behandlungseffekt interessiert.
Etwas komplizierter wird es, wenn Drittvariablen ins Spiel kommen: Nehmen wir an, dass die untersuchte Grösse stark vom Geschlecht abhängt, was z.B. in medizinischen Studien häufig vorkommt. Hier liegen folglich zwei Schnittstellen vor, an denen das Geschlecht wirksam sein kann:
- Einerseits kann sich die Stärke oder sogar die Richtung des Behandlungseffektes ändern.
- Andererseits kann sich die Wirkung bereits auch auf das Basisniveau der Werte auswirken.
ANOVA mit Messwiederholung: Beispiel SPSS
Wir nehmen das eingangs präsentierte Beispiel zur Medikamentenstudie und fügen den Analysen die Dummy-Variable frau als eine Kovariate bei (das ist zulässig, weil 0/1 Variablen als metrisch behandelt werden dürfen). Im Ergebnisoutput sind für uns die beiden nachfolgenden Tabellen relevant:
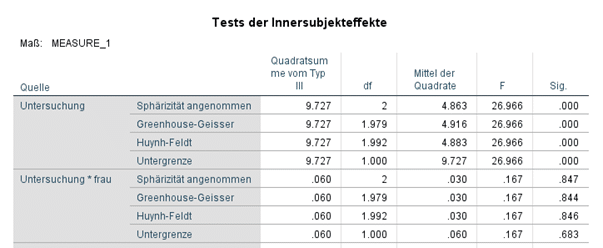
- Test auf Innersubjekteffekte: Die Signifikanzen (Sig.) der verschiedenen zur Verfügung stehenden Tests zeigen, dass die Behandlung einen signifikanten Effekt hat, das Frausein (Untersuchung*frau) sich aber auf diesen Effekt nicht auswirkt (hier in Form einer Interaktion spezifiziert).
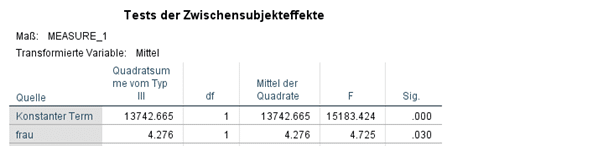
- Test der Zwischensubjekteffekte: Das Frausein (frau) wirkt sich hier signifikant (Sig.=0.030) auf das Basisniveau der gemessenen Werte aus.
Geht es lediglich um die Kontrolle der Variable Geschlecht, um einen unverzerrten Behandlungseffekt zu messen, sind diese Ergebnisse völlig ausreichend. Oft ist man aber genauer an den beiden Effekten der Drittvariablen interessiert und möchte diese in ihrer Stärke und Richtung beschreiben.
Hierfür bietet ANOVA für abhängige Stichproben nur begrenzte Möglichkeiten. In diesem Fall erscheint eine koeffizientenbasierte Modellierung (sogenannte gemischte Modelle) sinnvoller, wie wir nachfolgend zeigen wollen.
Linear mixed model als Alternative
Eine Messwiederholung stellt eine Variante der Clusterung von Messwerten dar. Somit handelt es sich faktisch um ein Mehrebenen-Design, wobei die Einzelmesswerte in der Stichprobe die erste Ebene darstellen und die wiederholt gemessenen Werte die zweite Ebene.
In einem linearen mixed model kann eine Studie mit mehreren Messzeitpunkten sehr einfach nachgebaut werden, indem man die abhängige Grösse auf die Zeitpunkt-Dummies regressiert. (Als Referenz nutzt man am besten den Ausgangzeitpunkt.)
ytk=(β0 + ζ0k) + (βttt + ζtk) + εtk
Mit Zeitpunkt t und Person k
Die Konstante entspricht dem allgemeinen Basisniveau der abhängigen Grösse, korrigiert um einen random intercept ζ0k. Diesen berechnen wir, indem wir davon ausgehen, dass Einzelmesswerte aufgrund unbeobachteter Eigenschaften systematisch unterschiedliche Basisniveaus aufweisen.
Die Koeffizienten der Zeitpunkte entsprechen den Behandlungseffekten zum jeweiligen Zeitpunkt, korrigiert um die random slopes ζtk. Diese berechnen wir, indem wir annehmen, dass aufgrund bestimmter unbeobachteter Personeneigenschaften die Behandlung sich systematisch unterschiedlich auswirkt.
Einzelne random effects dürfen auch ausser Acht gelassen werden. Je nach Annahme können wir somit das Modell schlanker oder komplexer gestalten. Diese detaillierten Möglichkeiten einer Spezifikation sind bei einer ANOVA nicht möglich.
ytk=(β0 + ζ0k) + (βttt + ζtk) + βixk+ βitxktt + εtk
Mit Zeitpunkt t und Person k und einer Drittvariable
Im nächsten Schritt ergänzen wir das Modell nun um eine Drittvariable und eine Interaktion zwischen dieser und jedem angeführten Zeitpunkt-Dummy. Der Haupteffekt der Drittvariablen stellt nun ihren Einfluss auf das Basisniveau dar, während die Interaktionseffekte in den Stichproben den Einfluss auf den Effekt der Behandlung zu unterschiedlichen Zeitpunkten darstellen.
Auch diese beiden Komponenten können prinzipiell um weitere random slopes korrigiert werden, so entsprechende Annahmen vorliegen.
Mixed models für abhängige Stichprobe: Beispiel SPSS
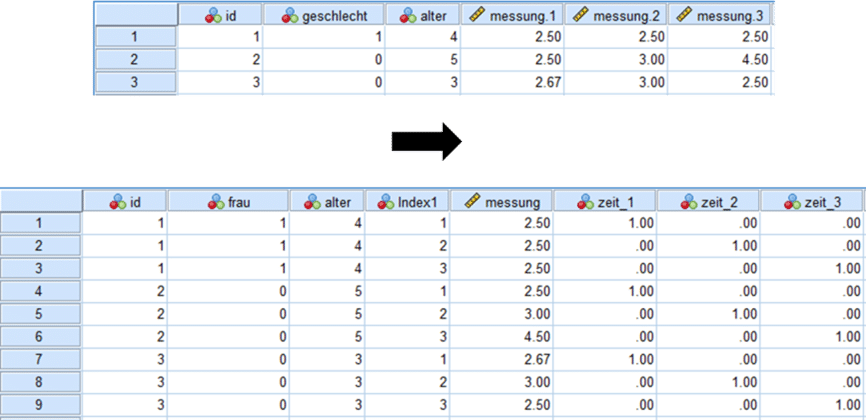
Da bei einem gemischten Modell nicht Personen, sondern Messungen untersucht werden, braucht man die Daten im sogenannten Long-Format. Diese erstellen wir in SPSS aus unserem vorherigen Datensatz mit der Funktion Daten –> Umwandeln.
Somit entsteht eine Indexvariable (index1), die die einzelnen Messungen kennzeichnet. Aus dieser bilden wir die Dummy-Variablen für die Zeitpunkte. Durch die Multiplikation mit der Variable frau entstehen die notwendigen Interaktionsvariablen.
Auf Basis dieser Daten wird nun ein random effect model berechnet. Wie das genau geht, haben wir im Detail bereits in einem früheren Artikel zu Mixed model Analyse beschrieben.
- Die Signifikanzen (Sig.) der Zeiteffekte zeit_2 und zeit_3 (Zeitpunkt 1 ist hier die Referenz) zeigen, dass die Behandlung einen signifikanten negativen Effekt hat. Bei den Interaktionstermen zeit2_frau und zeit3_frau wird zudem deutlich, dass das Frausein sich auf diesen Effekt nicht signifikant auswirkt.
- Der Haupteffekt der Variable frau zeigt, dass das Frausein sich signifikant positiv (allerdings auf einem 10% Niveau) auf das Basisniveau der gemessenen Werte auswirkt.
Die Ergebnisse ähneln also denen der ANOVA, die genauen Effekte können hier allerdings auch in ihrer Richtung und Grösse an den Regressionskoeffizienten abgelesen werden.
Ebenso sehen wir bei den Kovarianz-Parametern bzw. bei random intercept und random slopes, wie gross der Einfluss der unbeobachteten Verzerrer in Relation zur Gesamtvarianz ist (diese ergibt sich aus der Summe aller Komponenten). Der random intercept (Varianz=id) scheint beträchtlich zu sein.
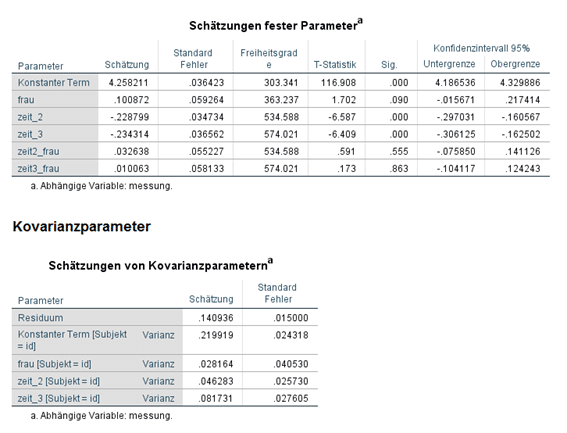
Die Einzelpersonen in den Stichproben weisen also grosse Basisunterschiede in den untersuchten Messwerten auf. Und auf die random slopes können wir bei weiteren Berechnungen durchaus verzichten.
Zusammenfassung und Fazit
Beide Verfahren, die ANOVA mit Messwiederholung sowie gemischte Modelle, liefern vergleichbare Ergebnisse. Vor allem bei der Verwendung von komplexeren Modellen mit Drittvariablen haben mixed models jedoch eindeutig Vorteile:
- ANOVA ist weniger übersichtlich. Regressionskoeffizienten stellen alle Einflüsse überschaubar nebeneinander dar.
- Richtung und Stärke der Einflüsse lassen sich bei einer ANOVA nur über zusätzliche aufwändige Berechnungsschritte ermitteln.
- Mixed models haben deutlich mehr Spezifikationsmöglichkeiten, die eine exaktere und efezientere Modellierung erlauben.
- Mixed models erlauben eine einfachere Varianzzerlegung, um den Einfluss der unbeobachteten Faktoren besser nachvollziehen zu können
- Lineare Modelle (zB. Generalised mixed models) lassen sich auch für nicht-metrische abhängige Stichprobe bzw. Variablen rechnen.
Und sobald Sie nun eine professionelle Hilfestellung bei der Auswahl und Anwendung einer passenden statistischen Methode benötigen, zögern Sie nicht und kontaktieren Sie uns! Nutzen Sie dazu gleich und unverbindlich unser Kontaktformular!
Quellen
- Zeitschrift für Klinische Psychologie und Psychotherapie
- Gabler Wirtschaftlexikon: Autokorrelation
- Dummy Variable: https://wlm.userweb.mwn.de/Ilmes/ilm_d6.htm