Gemischte Modelle, besser bekannt als mixed model, gehören zu jenen Analyseformen mit komplexen Daten, die nur selten in Statistikveranstaltungen präsentiert werden. Dieser Beitrag will diese Lücke schliessen und zeigen, dass dieses Verfahren sowohl leicht zu verstehen als auch genauso leicht anzuwenden ist. Wir demonstrieren eine Mixed Model Analyse an einem Anwendungsbeispiel zur Berechnung von einem random effects model im Statistikprogramm SPSS. Darüber hinaus erfahren wir auch einiges zur begrifflichen und methodischen Abgrenzung, vor allem zum Konzept der Panelanalyse sowie zu fixed effects models.
Sie benötigen Unterstützung bei der Aufstellung von gemischten Modellen und bei der Durchführung von mixed Modells mittels SPSS. Wenden Sie sich hierfür gerne an uns für eine professionelle Beratung.
Was wird in einem mixed model gemischt?
Vorweg, die Zusammenhänge zwischen Variablen drückt man in statistischen Analysen in Form von Kennzahlen bzw. Parametern aus. So berechnen wir in einer linearen Regression eine Konstante sowie Regressionskoeffizienten, die entsprechend die Basis der abhängigen Variablen und den Einfluss der unabhängigen Variablen auf sie darstellen. In den meisten Fällen bleiben diese Parameter konstant bzw. fix. Das bedeutet, dass sie für alle Elemente in der Stichprobe (und damit auch hochgerechnet für die Grundgesamtheit) gleich bleiben. Man bezeichnet sie daher als feste Effekte oder ‘fixed effects’.
Es kann nun aber sein, dass die Ausgangsniveaus und die Einflussstärken zwischen den Subjekten variieren. Zum Beispiel, wenn das Modell nur wenig relevante Informationen über die Elemente bzw. Parameter enthält. Ein einzelner fester Parameter würde die tatsächlichen Zusammenhänge dann nur ungenau oder gar falsch schätzen. Dann besteht die Möglichkeit, einen solchen variablen Effekt als eine Zufallsvariable mit einer gegebenen (meist normalverteilten) Verteilungsfunktion zu behandeln und jedem Element einen entsprechenden Wert zuzuweisen. Das bezeichnen wir als zufällige Effekte oder ‘random effects’.
Der Rest ist einfach und leicht umzusetzen: ein mixed model kombiniert nun die Berechnung von festen und zufälligen Effekten. Die häufigste (aber nicht einzige) Anwendung sind hier Paneldaten, wenn zum Beispiel jeder Befragte wiederholend Aussagen zu mehreren Zeitpunkten trifft. In solchen Fällen ist die Annahme der Unabhängigkeit der untersuchten Modellwerte meist verletzt, da Werte einer Person immer etwas ähnlicher, also tendenziell kleiner oder grösser als im Mittel sind. Dieses abweichendes Grundniveau kann man in einem random effects model berücksichtigen und neutralisieren.
Mixed Model in SPSS
Ein random effects model lässt sich einfach in SPSS berechnen. Stellen wir uns vor, eine Firma führt eine jährliche Mitarbeiterbefragung durch mit dem Ziel, die Zufriedenheit mit den Arbeitsprozessen zu erfassen und ggf. zu verbessern. Nun möchte die Fimenleitung analysieren, ob die Zufriedenheit (unter Kontrolle von Alter und Geschlecht) vom Lohn abhängt.
Mitarbeiter mit langjähriger Betriebszugehörigkeit haben folglich bereits wiederholt Angaben gemacht, was wir mithilfe eines zufälligen Effekts für die Konstante berücksichtigen wollen.
Auf der SPSS-Schaltfläche gehen wir auf: „Analysieren“ –> „Gemischte Modelle“ –> “Linear“
Im erscheinenden Fenster wählen wir die (eindeutige) Mitarbeiter-ID in das Feld „Subjekte“ und klicken auf „Weiter“. Weitere Felder sind für dieses Beispiel nicht relevant.
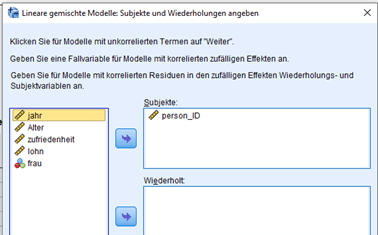
Im nächsten Fenster werden die abhängige sowie die unabhängigen Variablen definiert. Die kategoriale(n) Variable(n) (hier: Geschlecht) kommen zu den Faktoren, die metrischen (hier: Alter, Firmenzugörigkeit in Jahren, Einkommen) zu den Kovariaten, wie wir dies in einem früheren Beitrag zu ANOVA mit Messwiederholung bereits erklärt haben. Es ist üblich, in einer Panelanalyse SPSS auch immer den Befragungszeitpunkt (also den reinen Trendeffekt) zu kontrollieren, hier also das Jahr.
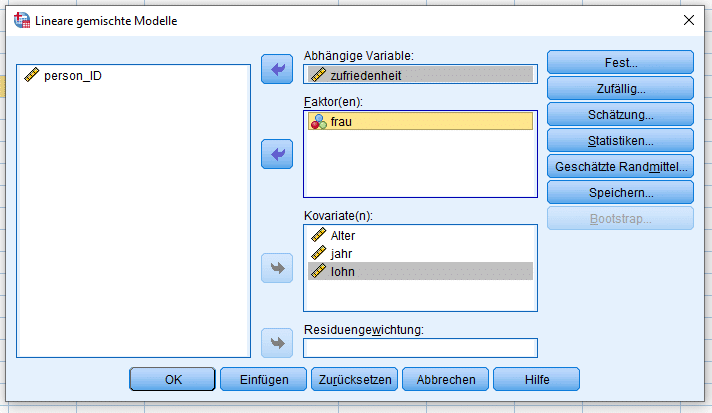
Fixed effects und Random effects in SPSS
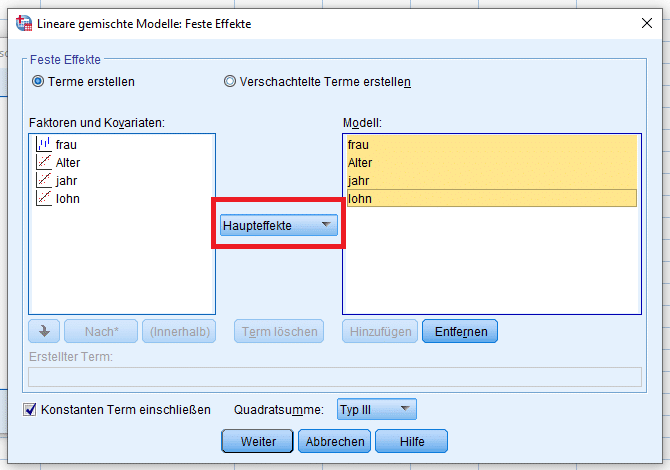
Als Nächstes müssen wir die festen und die zufälligen Effekte definieren. Im Fenster „Fest“ wählen wir alle Kovariablen in das rechte Fenster und geben an, dass wir nur Haupteffekte ohne Interaktionen berechnet haben wollen.
Im Fenster „Zufällig“ geben wir an, dass ein random effect für die Mitarbeiter-ID berechnet werden soll. Wichtig hierbei ist, den konstanten Term per Klick in das Modell aufzunehmen. Die Effekte der Kovariaten sollen fest bleiben, also ignorieren wir das obere Fenster. (Es ist aber grundsätzlich möglich, diese auch als variabel zu behandeln, falls Anlass zu einer entsprechenden Annahme besteht.)
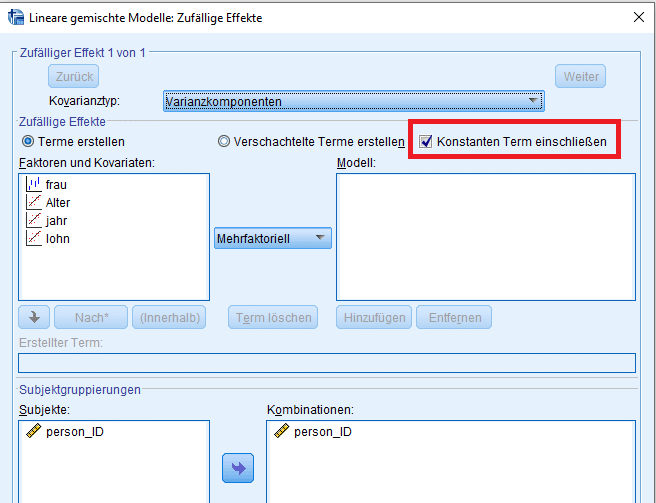
Zusätzlich klicken wir im Fenster „Statistiken“ auf „Parameterschätzung für feste Effekte“:
Haben wir das Modell definiert und auf „OK“ gedrückt, erscheint das Ergebnis im Ausgabefenster. Auch im Rahmen einer Panelanalyse SPSS präsentiert das Programm wie üblicher viele Einzelberechnungen. Für unsere Analyse ist nachfolgender Abschnitt des Outputs wichtig:
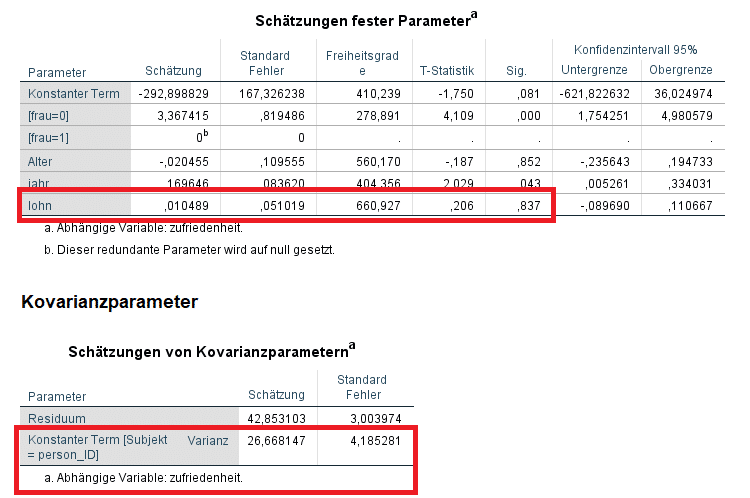
Die Koeffizienten der festen Effekte interpretieren wir analog zu einer gewöhnlichen linearen Regression. Im Beispiel zeigt sich etwa, dass Lohn und Alter keinen signifikanten Einfluss auf die Zufriedenheit der Mitarbeiter haben, das Geschlecht allerdings schon (sig.). Die personenspezifischen Abweichungen sind hier bereits berücksichtigt. Es handelt sich also um einen dem Paneldesign gegenüber robusten Koeffizienten.
Sie benötigen Hilfe bei der Analyse komplexer Daten mittels mixed model bzw. bei der Durchführung einer Panelanalyse SPSS? – Nähere Informationen erhalten Sie bei unseren Experten in der SPSS Hilfe!
Panelanalyse SPSS: Interpretation der Varianzkomponenten
Der zufällige (ramdomisierte) Effekt ist im Ouptut unten zu finden unter: ‘Konstanter Term [Subjekt Varianz]’. – Was bedeutet aber nun diese Zahl 26,67…?
Im Gegensatz zu einem einfachen linearen Modell hat das vorliegende Modell keine feste Konstante mehr. Der abgebildete Term ist lediglich das Ausgangsniveau, zu dem wir für jedes Subjekt einen bestimmten Wert aufsummieren oder abziehen müssen. Das Programm weist also jeder Person eine eigene „Konstante“ zu und diese vielen „Konstanten“ gleichen die nicht erfassten Unterschiede zwischen den Personen aus. Hier wird die Varianz ihrer Verteilung dargestellt.
Die Varianz der Residuen repräsentiert den Restfehler des Models, die Summe der beiden Komponenten hier ist die gesamte Modellvarianz, die nicht durch die festen Effekte im Modell erklärt werden kann. Das Verhältnis der beiden Komponenten zeigt an, auf welcher Ebene die Unterschiede in der Zufriedenheit angesiedelt sind.
Wir sehen, dass etwa 38% der Modellvarianz auf die Personenebene zurückgehen [Berechnung: 26,7/(26,7 + 42,3)*100]. Anders formuliert: Rund 38% lassen sich also allein auf die unterschiedliche Einstellung der einzelnen Mitarbeiter zurückführen. Dieser Wert sollte sich reduzieren, wenn wir weitere relevante Informationen in das Modell aufnehmen. In einem guten Modell sollte der Residualterm im Verhältnis zur einfachen Varianz der anhängigen Variablen möglichst klein sein.
Rund um Mixed Models: Begriffsklärung
Es gibt eine Reihe an Begriffen, die im Zusammenhang mit mixed model immer wieder auftauchen und teilweise unterschiedlich gebraucht werden. Um Verwirrung zu vermeiden, schauen wir uns die drei häufigsten Fälle kurz an:
- Panelanalyse: Ein Panel ist eine sich wiederholende Erhebung derselben Stichprobenfälle (zB. Personen bzw. Mitarbeiter wie im dargestellten Beispiel). Der Begriff Panelanalyse SPSS bezieht sich auf diese Datenstruktur und nicht explizit auf eine bestimmt Analysemethode. Gemischte Modelle sind dabei eine häufige aber nicht ausschliessliche Analyseanwendung.
- Fixed effects model: Dieser Modelltyp ist eine weitere sehr beliebte Analysemethode von Paneldaten. Es ist jedoch kein mixed model und basiert ausschliesslich auf festen Effekten. Dabei nimmt man Dummy-Variablen für jedes Element in das Modell auf (in unserem Fall Personen-Dummies). Die Bezeichnung fixed effects bezieht sich dabei speziell auf die Koeffizienten dieser Dummy-Variablen. Durch diese Vorgehensweise werden alle Unterschiede zwischen den Personen eliminiert. In unserem Beispiel hätten wir also lediglich den Einfluss der Lohnveränderungen über die Zeit gesehen, die Lohnunterschiede zwischen den Personen wären unterdrückt.
- Mehr-Ebenen-Analysen: Mehr-Ebenen-Design bezieht sich wiederum auf eine bestimmte Datenstruktur, bei der Beobachtungen geclustert, also in Einheiten einer höheren Ebene gruppiert sind. Dazu gehören auch Paneldaten (Clusterung der Einzelbeobachtungen innerhalb von Subjekten), meistens ist damit aber die regionale Clusterung oder mehrstufige Stichproben gemeint.
Fazit: Mixed Model SPSS
Nach möglichen Einstiegshürden erweisen sich gemischte Modelle als eine leicht anwendbare und auch in SPSS einfach umsetzbare Option, die vor allem bei einer komplexen Datenstruktur interessant ist. Wie jedes andere Modell basieren aber auch mixed models auf Annahmen, die sich auf ihre Interpretation auswirken.
Ob am Ende ein random effects model, ein fixed effects model oder eine einfache (lineare) Regression durchgeführt wird, hängt schliesslich vom Forschungsinteresse und der spezifischen Forschungsfrage ab. Es ist aber immer vom Vorteil, das Gesamtportfolio an Möglichkeiten zu kennen, um daraus die beste und aussagekräftigste Methode und Herangehensweise auswählen und anwenden zu können. Bei konkreten Fragen zu den jeweiligen Verfahren kontaktieren Sie uns gerne unverbindlich über das Anfrageformular!