Die Vielfalt statistischer Methoden ist Segen und Fluch zugleich. Der Segen ist, dass für nahezu alle Fragestellungen und Datengrundlagen ein passendes Verfahren existiert, das ein aussagekräftiges und valides Ergebnis liefert. Die Herausforderung liegt in der Notwendigkeit, die Vielfalt an Methoden zu kennen, um daraus das bestmögliche Verfahren auszuwählen. Gerade das Statistik-Programm SPSS bietet sehr breite Anwendungsmöglichkeiten für eine multivariate Analyse. Die mit der Zeit breit gewachsene Benutzeroberfläche – die nicht immer einer stringenten Logik folgt – könnte den ungeübten Anwender zunächst aber schnell überfordern. Folglich wollen wir am Beispiel Lineares Modell und Gemischtes Modell etwas Klarheit dazu schaffen.
Sie möchten eine multivariate Analyse für lineare gemischte Modelle mittels SPSS umsetzen und benötigen Unterstützung bei der Wahl und Durchführung eines geeigneten Verfahrens? Wenden sie sich hierzu an uns für eine professionelle Beratung.
Der folgende Artikel will einen Überblick über einige wesentliche multivariate Verfahren geben, die mittels SPSS analysierbar sind, und beantwortet im wesentlichen folgende Fragen:
- Was ist die Grundidee für eine multivariate Analyse?
- Was sind lineare bzw. gemischte Modelle und wo finde ich in SPSS: Allgemeines lineares Modell?
Folgende Bereiche der SPSS-Maske wollen wir daher im Detail besprechen:
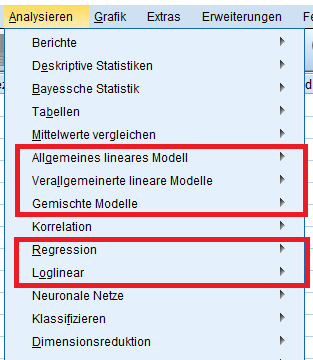
Multivariate Analyse: Grundidee
Ziel einer multivariaten Analyse ist es, einen Zusammenhang zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen zu beschreiben und zu prüfen. Je nach genutzter Methode berechnen wir bestimmte Parameter und nutzen in der Folge inferenzstatistische Methoden, um Aussagen über Vorhandensein, Stärke, Richtung und Generalisierbarkeit der Zusammenhänge zu treffen. Eine Sonderform bildet dabei die Regression, bei der man die abhängige Grösse über mathematische Berechnungen aus den unabhängigen Variablen schätzt.
Ausnahmslos alle statistischen Methoden basieren auf Annahmen, die man zuvor prüfen sollte. Sind die Voraussetzungen nicht erfüllt, gilt es Anpassungen vorzunehmen (zB. eine andere Methode zu wählen), um aussagekräftige und gültige Ergebnisse zu erhalten. Eine der wichtigsten Annahmen betrifft das Skalenniveau der abhängigen Variablen, dieses wird auch meistens als erstes festgelegt. Aus diesem Grund wird die Unterscheidung einzelner Verfahren sehr oft entlang dieses Kriteriums vorgenommen.
Allgemeines lineares Modell: Varianzanalyse & Regression
Ein allgemeines lineares Modell (general linear model) in ihrer vielfältigen Form kann man in gewisser Weise als Ausgangsform für eine multivariate Analyse bezeichnen. Man wendet sie an, wenn die abhängige Variable metrisch ist. Eine Ausnahme bilden die linear probability models, hier kann man den Einfluss sowohl von metrischen als auch von kategorialen unabhängigen Variablen untersuchen.
Der Zusammenhang wird zunächst linear modelliert. Das heisst: die abhängige Grösse wird als lineare Funktion der unabhängigen Variablen geschätzt. Das gibt der Modellgruppe ihren Namen. Etwas irreführend ist, dass SPSS unter dem Reiter Allgemeines lineares Modell lediglich unterschiedliche Formen der Varianzanalyse zusammenfasst. Wichtig zu merken: multivariat bezieht sich bei der Varianzanalyse stets auf die abhängigen Variablen.
In SPSS: Allgemeines lineares Modell sind folgende Verfahren zu finden:
- ‘einfache’ ANOVA: die klassische Varianzanalyse mit kategorialen unabhängigen Variablen sowie ANCOVA als Kovarianzanalyse mit metrischen unabhängigen Variablen
- MANOVA und MANCOVA: diese zielen auf die Analysen mit mehreren abhängigen Variablen ab. Nicht zu verwechseln: multivariat bezieht sich bei der Varianzanalyse auf die abhängigen Variablen
- Varianzanalyse für Daten mit Messwiederholungen
Zur Ergänzung: Die lineare Regression dagegen als einer der wichtigsten Vertreter in dieser Gruppe von Methoden findet sich bei SPSS unter dem (eigenen) Pfad Regression.
Wir unterstützen Sie gerne bei der Auswahl eines passenden Verfahrens in SPSS für Ihre Fragestellung und bei der Umsetzung der Analysen. Kontaktieren Sie uns unverbindlich über unser Kontaktformular.
Verallgemeinertes lineares Modell
Lineare Modelle verlangen also eine metrische abhängige Variable. Messtheoretisch bedeutet das, dass niedrigere Skalenniveaus Werteabstände nicht erfassen können. Genau das drückt aber ein linearer Parameter aus. Des weiteren wird die Annahme der Normalverteilung der Residuen bei Variablen mit nur wenigen Ausprägungen nahezu immer verletzt. Auch das ist eine der grundlegenden Annahmen für die inferenzstatistische Generalisierung der Modellergebnisse. In bestimmten Fällen kann dieses Problem auch bei metrischen Variablen vorkommen, wie zum Beispiel bei Zähldaten.
Die Gruppe der verallgemeinerten linearen Modelle (generalised linear models) umfasst nun Verfahren, die auf solche Fälle zugeschnitten sind. Je nach Anwendung können damit binäre, kategoriale, ordinale oder abgezählte abhängige Variablen untersucht werden.
Der Trick besteht darin, dass man eine latente Grösse schätzt, die mit den unabhängigen Variablen in einem linearen Verhältnis steht. Daher auch der Name verallgemeinert linear. In einem zweiten Schritt werden die erwarteten Werte der abhängigen Grösse mithilfe einer weiteren nicht linearen Funktion aus dieser latenten Variablen geschätzt. Diese Funktion nennt man Linkfunktion. Die Berechnung der Parameter beider Funktionen geschieht meistens mir der Maximum-Likelihood Methode.
Die meisten Anwendungen dieser Art fasst SPSS unter dem Pfad Verallgemeinerte lineare Modelle zusammen. Aber auch hier befindet sich analog zu oben die binärlogistische Regression, eines der beliebtesten solcher Verfahren, unter dem Reiter Regression. Auch Loglineare Modelle, die eine Sonderform der verallgemeinerten linearen Modelle darstellen und Zusammenhänge zwischen nominalskalierten Variablen untersuchen, sind in einer eigenen Kategorie ausgegliedert.
Gemischtes Modell
Gemischte Modelle (mixed model) befinden sich in der SPSS-Maske in einer Reihe mit den allgemeinen und verallgemeinerten linearen Modellen. Dabei steht ein gemischtes Modell nicht ergänzend, sondern überlappend zu den beiden Methodengruppen. Denn ihre Anwendung zielt nicht ab auf die Skalierung der abhängigen Variablen, sondern auf die potentielle Abhängigkeit ihrer Werte.
Wie wir in einem anderen Artikel zur Mixed Model-Analyse erklärt haben, kann es durch die systematische Häufung der Beobachtungen (z.B. bei Messwiederholungen) zu einer Verletzung der Annahme des unabhängigen Modellfehlers kommen. Um das zu beheben, modelliert man einen sogenannten zufälligen Effekt (random effect), also eine nach vorgegebener Form verteilte Zufallsvariable, die die systematischen Abweichungen auffängt. Die Aufnahme eines solchen zufälligen Effektes in ein Modell, das an sich nur feste Parameter hat, macht es zu einem gemischten Modell.
Gemischte Effekte können wiederum in unterschiedliche Modelltypen aufgenommen werden. So bietet SPSS Optionen sowohl für allgemeine wie auch für verallgemeinerte lineare Modelle.
Ergänzend sei angemerkt, dass ein gemischtes Modell nicht allgemein mit Panelanalysen verwechselt werden darf, denn hier wendet man neben dem random effect-Modell auch gerne das sogenannte fixed effect-Modell an. SPSS hat aktuell kein gesondertes Tool für Panelanalysen. Fixed effect-Modelle muss man daher eigenhändig durch die Modellierung von entsprechenden festen Grössen (mittels der Dummy-Variablen) durchführen.
Wer in SPSS nach Mehrebenen-Modellen bzw. hierarchischen (linearen) Modellen sucht, wird zumindest unter diesen Begriffen nicht fündig werden. Ein Mehrebenen-Modell ist nämlich streng genommen ein gemischtes Modell mit zufälligen Effekten für die Aggregationsebene(n).
Fazit
Das Ziel dieses Beitrags war es, einen Einblick in die unter Analysen in SPSS aufgelisteten Modellgruppen für eine multivariate Analyse zu geben. Für den Anwender ist im ersten Schritt weniger entscheidend, wie genau die eine oder andere Berechnung funktioniert. Viel wichtiger ist es, zu erkennen, welche Anwendung bestmöglich zur eigenen Fragestellung und zum erstellten Forschungsdesign passt. Ist die Wahl getroffen, folgt die vertiefende Einarbeitung. Wenn Sie nun professionelle Hilfe bei der Auswahl und Anwendung einer statistischen Methode wünschen, kontaktieren Sie unsere Statistikberatung!