In früheren Beiträgen haben wir bereits die Umsetzung einer Moderationsanalyse mithilfe modellierter Interaktionen behandelt. Der Fokus lag hier auf der Umsetzung mit Statistikprogrammen, zB. Moderation mit SPSS und Interaktionseffekte in Stata. Darüber hinaus haben wir einige grundlegende Interpretationshinweise aufgezeigt. Allerdings fällt es teilweise auch mit Vorkenntnissen oft schwer, den Haupteffekt und die Interaktionseffekte auf einen Blick intuitiv zu lesen und voneinander zu unterscheiden, vor allem wenn einer der Koeffizienten nicht signifikant ist.
Sie möchten eine Interaktionsanalyse durchführen und Haupt- und Interaktionseffekte interpretieren? Wenden sie sich hierzu an uns für eine professionelle Beratung.
Mit diesem Beitrag wollen wir auf folgende spezifischen Fragen eingehen:
- Was ist eine Interaktion in einer Moderationsanalyse?
- Was ist ein Haupteffekt und welche Arten von Effekten gibt es?
- Wie kann man Haupteffekte interpretieren?
Zur Wiederholung: Was ist eine Interaktion?
Ein (einfacher) Interaktionseffekt ist eine technische Repräsentation einer Moderationsanalyse. Eine Moderation liegt vor, wenn die Stärke des Effektes einer unabhängigen Variablen von der Ausprägung einer anderen unabhängigen Variablen beeinflusst wird.
Formal wird ein Interaktionseffekt in einer Regressionsformel – hier in der linearen Version – folgendermassen dargestellt:
Y = sso + ss1*X1 + ss2*X2 + ss3*X3 + ss4*X2*X3Hier umgesetzt an einem leicht angepassten Beispiel aus dem erwähnten früheren Beitrag:
debt= sso + ssinvest*invest + sssize*size + sslisted*listed + ssinter*size*listedIn diesem Beispiel hat die Variable invest (Investitionsvolumen) einen festen, also nicht veränderbaren Einfluss auf debt (Verschuldungsgrad eines Unternehmens), der durch den Koeffizienten ssinvest beschrieben wird. Der Einfluss der Variable size (Grösse) ist dagegen nicht fix. So müssen wir bei der Berechnung der Schätzwerte von debt der Komponente sssize *size auch den Wert der Komponente ssinter *size*listed hinzufügen.
Dieser Wert hängt allerdings von der Ausprägung von listed (börsennotiert ja/nein) ab. Das bedeutet folglich, dass wir bei konstanter Unternehmensgrösse, abhängig von der Ausprägung von listed, unterschiedlich viel hinzu zu rechnen haben. Formal gesehen entspricht das der Formulierung: Der Effekt von size ist abhängig von der Ausprägung von listed.
Mathematisch betrachtet erscheint eine Interaktion immer symmetrisch, d.h. jede der beteiligten Variablen moderiert folgerichtig die Wirkung der jeweils anderen Variablen. Konkret in unserem Fall: die Ausprägung size beeinflusst auch den Effekt von listed. Welche der beiden Moderationen inhaltlich Sinn ergibt, ist eine Frage der Interpretation und hängt von der Fragestellung ab.
Nachfolgend ist ein solcher Interaktionseffekt grafisch dargestellt:
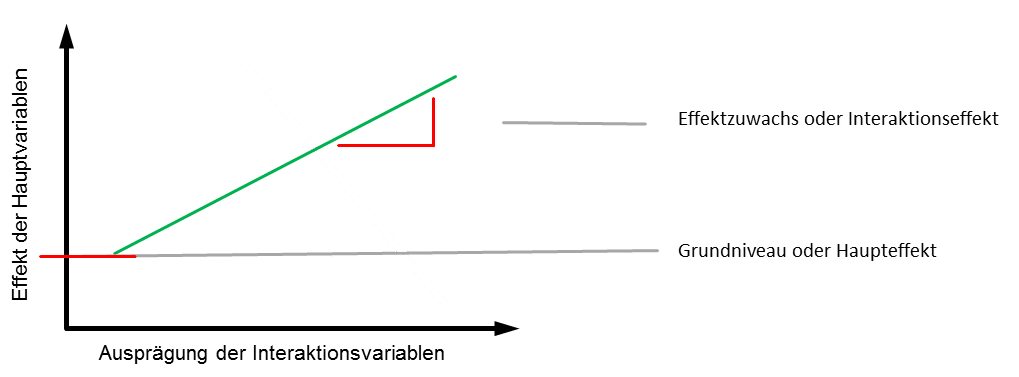
Haupteffekt: Definition und Arten von Effekten
Wir können insgesamt drei Arten von Effekten unterscheiden, marginaler Effekt, Haupteffekt und Interaktionseffekt:
- Marginaler Effekt: in unserem Beispiel ist das ssinvest , sprich: mit einer zusätzlichen Einheit von invest wächst debt genau um diesen Wert. Dieser Effekt ist fix und gilt für alle Kombinationen der Kovariablen im Modell.
- Haupteffekt (bei einer Interaktionsbeziehung; sssize in unserem Beispiel): Eine passendere Bezeichnung wäre eigentlich Basiseffekt, denn es ist der Effekt von size im Falle, wenn die Interaktionsvariable invest den Wert Null hätte. Dieser Fall ist empirisch oft unmöglich bzw. nicht gegeben (Alter, Einkommen). Bei einer Dummy-Variablen wie im vorliegenden Fall entspricht dieser Wert der Referenzkategorie. Ganz wichtig: bei einer Interaktionsbeziehung gibt es nicht mehr einen Effekt, der Haupteffekt ist lediglich Ausgangswert für die Berechnung des spezifischen Effektes.
- Interaktionseffekt: von solchen spezifischen Effekten gibt es genau so viele wie es Ausprägungen der Interaktionsvariablen gibt. Die Spannweite reicht als demnach von zumindest zwei (bei einer Dummy-Variablen) bis zu Hunderten (bei einer metrischen Variablen mit vielen Einzelausprägungen). Den spezifischen Effekt von size berechnet man dann als: sssize + sssize *listed. Der Term sssize ist dann der eigentliche Interaktionseffekt.
Novustat verfügt über ein erfahrenes Team an Statistikern, die Ihnen persönlich und unkompliziert zur Verfügung stehen. Schicken Sie uns einfach Ihre Anfrage! Wir beraten Sie gerne, sowohl für eine Moderationsanalyse als auch zur Ermittlung von Haupteffekt und Interaktionseffekten.
Haupteffekt und Interaktion interpretieren
Insbesondere bei einer metrischen Interaktionsvariablen verzichtet man oft darauf, einzelne Schätzwerte zu berechnen und zu vergleichen. Deutlich einfacher ist es, die Richtung des Interaktionskoeffizienten und sein Verhältnis zum Haupteffekt zu interpretieren.
Haupteffekte interpretieren wir wie folgt: Wenn die Richtung (ablesbar am Vorzeichen) des Interaktionskoeffizienten mit dem des Haupteffektes übereinstimmt (positives Vorzeichen), dann verstärkt die Interaktionsvariable den Haupteffekt. Eine entgegengesetzte – negative – Richtung bedeutet, dass der Haupteffekt abgeschwächt wird.

Diese verstärkende bzw. abschwächende Wirkung ist umso stärker, je grösser das Verhältnis der Interaktionsstärke zum Haupteffekt ist (also ssinter* listed/ sssize in unserem Beispiel). Bei einer besonders starken entgegengesetzten Interaktion ist es auch möglich, dass dieses Verhältnis grösser als 1 wird und der Effekt dadurch „umgedreht wird“ bzw. kippt und das Vorzeichen wechselt (siehe nachfolgende Abbildung).
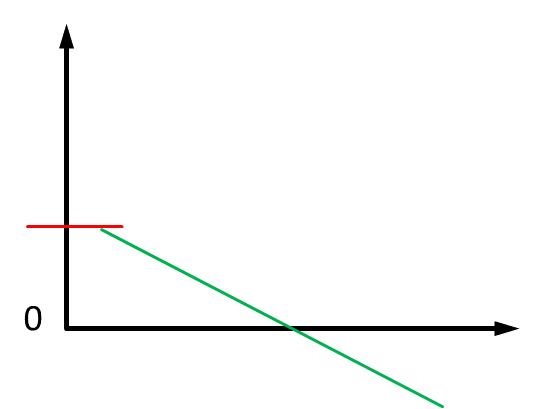
Haupteffekte interpretieren: Signifikanz
Nicht weniger wichtig ist die Signifikanz der beiden Komponenten, wenn wir die Haupteffekte interpretieren. Die Koeffizienten an sich sind lediglich deskriptive Masse. Ein statistischer Test prüft, ob diese Beziehung auch verallgemeinerbar ist.
Die Ergebnisse zur Signifikanz lassen sich wie folgt in Bezug auf die Haupteffekte interpretieren:
- Sollte der Interaktionskoeffizient nicht signifikant (hier ssinter) sein, dann entspricht der Haupteffekt einem marginalen Effekt und sollte als fix behandelt werden.
- Ist der Haupteffekt nicht signifikant (hier sssize), ist die Interpretation etwas komplexer: Ein nicht signifikanter Haupteffekt bedeutet, dass die Hauptvariable genau dann keinen Einfluss hat, wenn die Interaktionsvariable den Wert “Null” besitzt. Die Interaktionsbeziehung kann jedoch weiterhin bestehen (= signifikanter Interaktionskoeffizient). Da der Effekt (bzw. die Effektstärke) der Hauptvariablen dadurch gegebenenfalls wächst, ist es möglich, dass dieser ab einem gewissen Niveau signifikant wird. Möchte man diese Grenze erfahren, kann zum Beispiel der sogenannte “MER” (marginal effect at specific values) berechnet werden.
- Ein nicht signifikanter Einfluss der Interaktionsvariablen (hier sslisted) ist dageben unproblematisch. Eine Variable kann den Effekt einer anderen Variablen beeinflussen, ohne selber einen marginalen Effekt zu haben.
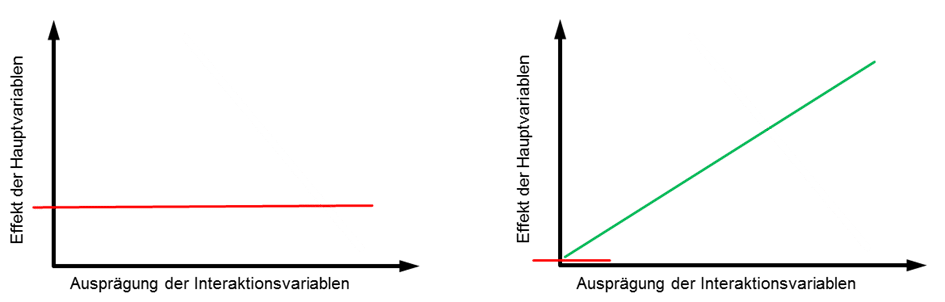
Fazit
Der Artikel zum Thema Moderationsanalyse verdeutlicht augenscheinlich wie herausfordernd es sein kann, wenn man Haupteffekte interpretieren will und den Einfluss von Interaktionseffekten berücksichtigen muss, vor allem wenn man auch ihre Signifikanzen in Betracht zieht. Mit diesem Beitrag haben wir Ihnen einige wichtige und hilfreiche Interpretationshinweise dafür an die Hand gegeben.
Eine ausführliche Interpretation von Haupteffekt und Interaktionen am Beispiel einer Faktorenanalyse finden Sie ergänzend hier.
Wenn Sie professionelle Hilfe zum Thema “Haupteffekte interpretieren” brauchen, wenden Sie sich hierzu gerne an uns für eine Beratung und schicken Sie uns unverbindlich eine schriftliche Kontaktanfrage.