Viele Anwender erlernen statistische Modellierung ausgehend von lineareren Modellen. Damit passiert oft der Fehlschluss, bei der Anwendung eines nicht-linearen Modells die Parameter auf die gleiche Weise zu interpretieren, was zu groben Fehlinterpretationen führen kann. Margins Stata bietet eine effektive Möglichkeit, auf die Besonderheiten von nicht-linearer Modellierung einzugehen. Aber auch für lineare Modelle bietet das Tool zusätzliche Optionen für die Interpretation und Darstellung von Modellergebnissen.
Sie möchten nicht lineare Modelle mittels Margins Stata einfach und aussagekräftig interpretieren und visualisieren? – Dannn wenden sie sich hierzu an uns für eine professionelle Statistik Beratung!
Was bedeutet margins?
Mit margins gibt Stata die Vorhersage des Modells, also die Schätzung der abhängigen Grösse, in Abhängigkeit von den Werten einer oder mehreren Kovariablen aus. Damit kann man sowohl exakte Vorhersagen bei bestimmten Werten der Kovariablen als auch die marginalen Veränderungen berechnen.
Ein solcher Marginaleffekt zeigt die Veränderung der abhängigen Grösse, gegeben die Veränderung der unabhängigen Grösse um eine Einheit. Mit margins in Stata kann man drei Arten von Marginaleffekten bestimmen:
- Average marginal effect (AME): Effekt einer Variablen, gemittelt über alle Ausprägungen der Kovariablen
- Marginal effect at the means (MEM): Effekt einer Variablen im Fall, wenn alle Kovariablen ihren mittleren Wert annehmen würden. Das ist oft allein aufgrund des Skalenniveaus der Kovariablen nicht gegeben. Bei manchen Fragestellungen lassen sich aber damit sinnvolle Aussagen machen.
- Marginal effect at representative values (MER): Effekt einer Variablen, wenn eine oder mehrere Kovariablen zusätzlich auf einen bestimmten Wert fixiert werden. Diese Anwendung ist vor allem bei Interpretation von Interaktionseffekten hilfreich.
Sonderfall: Nicht-lineare Modelle
In einer linearen Regression entspricht der Marginaleffekt dem Regressionskoeffizienten. Bei einem verallgemeinerten linearen Modell wird die relevante abhängige Grösse erst in einem zweiten Schritt funktional bestimmt.
So ist zum Beispiel in einer logistischen Regression der Marginaleffekt auf die Wahrscheinlichkeit, den abhängigen Zustand anzunehmen, noch nicht durch den Regressionskoeffizienten wiedergegeben. Er kann allerdings mit margins in Stata zusätzlich bestimmt werden.
Nicht-lineare Modelle haben darüber hinaus ein weiteres Problem, das margins löst. Die Skalierung der Koeffizienten (also die Bestimmung ihrer exakten Grösse) in einer linearen Regression geschieht über den Abgleich der Schätzwerte mit den empirischen Werten, also über die Residuen.
Die z-Werte einer logistischen Regression haben allerdings keine empirische Entsprechung und das Modell hat somit auch keine Residuen. Bei der Skalierung der Koeffizienten wird ihre (hypothetische) Streuung mit einem konstanten Parameter angegeben.
Da der tatsächliche Modellfehler je nach Modell (und sogar innerhalb eins Modells) variieren kann, sind die Koeffizienten in unterschiedlichen Modellen unterschiedlich skaliert und dürfen somit nicht verglichen werden. Bei den Marginaleffekten ist das allerdings schon möglich und zulässig.
Schliesslich wird oft vergessen, dass die lineare Verrechnung der Interaktionskoeffizienten in den nicht-linearen Modellen nicht sinnvoll möglich ist und damit z.B. ein Interaktionskoeffizient an sich nicht aussagekräftig ist.
Die Grösse des Interaktionseffekts und seine Signifikanz kann in nicht-linearen Modellen nämlich je nach der Ausprägung der beiden Interaktionsvariablen variieren. Margins bietet eine gute Möglichkeit, auch solche Modelle sinnvoll zu interpretieren.
Margins in Stata: Anwendungsbeispiel
In Stata lassen sich margins mit einem postestimation-Befehl (Übersicht siehe Anhang) direkt nach einer Regression berechnen. Wir nehmen hier das (fiktive) Beispiel einer logistischen Regression für das hohe Berufsengagement in Abhängigkeit von Geschlecht und Alter.
Das Engagement wird binär mit 1 (vorhanden) du 0 (nicht vorhanden) gemessen.
logit engagement i.frau alter
Margins Stata: Verteilung des Effektes über den Wertebereich
In einem linearen Modell trägt die Steigerung der unabhängigen Variablen immer gleich viel zur Veränderung der abhängigen Variablen bei. Nicht so in nicht-linearen Modellen, hier ist der berechnete Marginaleffekt lediglich das Mittel aus variierenden Effekten, die über den gesamten Werteberreich der unabhängigen Grösse verteilt sind.
Als solcher bietet er bereits eine sinnvolle Aussage, manchmal ist man aber an dem genaueren Effektverlauf interessiert. Diesen stellen wir jetzt für die Variable Alter dar, indem wir die vorhergesagten Wahrscheinlichkeiten für hohes Berufsengagement für die Alterswerte zwischen 18 und 38 (in Fünferschritten) berechnen und ihre Verteilung anschliessenden mit dem Befehl marginsplot grafisch darstellen lassen.
logit engagement frau alter
margins, at(alter=(18(5)38))
marginsplot
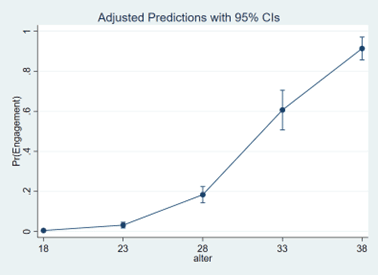
Solche Schätzwerte der abhängigen Grösse bei variablen Werten der unabhängigen Grösse bezeichnet Stata als predictive margins.
Margins in Stata: Modellvergleich
Nutzen wir nun den margins Befehl für den Vergleich von zwei Modellen. Wir wollen im Rahmen einer Mediationsanalyse erfahren, ob das Alter einen möglichen Geschlechtereffekt hat und brauchen daher ein Modell mit und ohne Altersvariable.
Wir wollen jedoch keine predictive margins, sondern einen Marginaleffekt für alle Variablen im Modell ausgeben. Die AME erhält man durch die Option dydx(VAR), die MEM mit der zusätzlichen Option atmeans.
Für eine bessere Gegenüberstellung exportieren wir den berechneten AME in eine APA-Tabelle, indem wir den Zusatz stata margins post in Kombination mit einem Exportbefehl nutzen, konkret:
logit engagement frau
eststo margin: margins, dydx(*) post
est sto m1
logit engagement frau alter
eststo margin: margins, dydx(*) post
est sto m2
esttab m1 m2Das (annähernd) publikationsfertige Ergebnis sieht dann wie folgt aus:

Margins Stata: Interaktionen veranschaulichen
In einem früheren Beitrag zu Interaktionseffekte in Stata haben wir bereits die Darstellung von Interaktionsbeziehungen mithilfe von margins Stata als eine übersichtliche Interpretationsgrundlage vorgestellt. Diese Darstellung ist aber nicht immer vorteilshaft.
Bei nicht-linearen Modellen ist sie in der tabellarischen oder grafischen Form aus oben genannten Gründen notwendig. Wichtig, bei der Berechnung von Interaktionen in Kombination mit margins darf man die Faktoren-Schreibweise nicht vergessen.
Ein Beispiel für die Interaktion einer binären und einer metrischen Variablen sieht folgendermassen aus:
logit engagement i.frau##c.alter
margins frau, at(alter=(18(5)38))

marginsplot
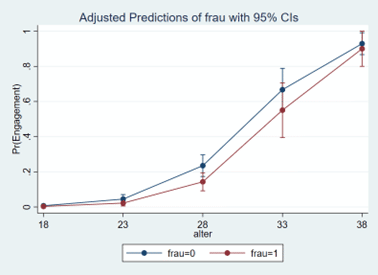
Fazit
Mit margins bietet Stata ein Tool, das vor allem in SPSS stark vermisst wird. Die Benutzung ist nicht immer ganz intuitiv, und der Einstieg kann sich eventuell etwas schwierig gestalten. Mit diesem Beitrag wollen wir interessierten Nutzern diesen Einstieg erleichtern.
Wichtig zu ergänzen ist, dass die Anwendung von Marginaleffekten in nicht-linearen Modellen mittlerweile als Standard gilt. Wer binäre Outcomes untersuchen und nicht auf andere Methoden, zum Beispiel auf ein linear probability model, ausweichen möchte, sollte sich für Modellvergleiche und/oder Interaktionsanalysen diese Schritte aneignen bzw. auf alternative Anwendungen (Beispiel siehe ‘Weiterführende Links’) zurückgreifen.
Bei weiteren Fragen und Unterstützungsbedarfen freuen wir uns über Ihre unverbindliche Kontaktaufnahme über unser Anfrageformular. Gerne erstellen wir Ihnen umgehend unverbindlich ein massgeschneidertes Angebot!
Weiterführende Links und Literaturtipps
- Übersicht über postestimation-Befehle
- Faktoren-Schreibweise
- linear probability model
- Beispiel für alternative Anwendungen: Computing interaction effects and standard errors in logit and probit models
- Ai, Chunrong; Norton, Edward C. (2003): Interaction terms in logit and probit models. In: Economics Letters 80 (1), S. 123–129. DOI: 10.1016/S0165-1765(03)00032-6.
- Mood, Carina (2010): Logistic regression. Why we cannot do what we think we can do, and what we can do about It. In: European Sociological Review 26 (1), S. 67–82.