Ein Post Hoc Test soll signifikante Unterschiede zwischen verschiedenen Gruppen aufspüren und analysieren. Somit gehört der Post Hoc Test zur Gruppe der Signifikanztests. Dabei können wir zum einen feststellen, ob es signifikante Unterschiede gibt, und zum anderen auch, zwischen welchen Datengruppen diese bestehen.
Das Feld der Post Hoc Tests ist nicht immer ganz einfach zu verstehen. Sollten Sie Unterstützung bei der Durchführung und Interpretation eines Post Hoc Tests benötigen, dann wenden sie sich hierzu an uns für eine professionelle Statistik Beratung!
Was genau macht der Post Hoc Test?
Post Hoc Tests kommen etwa in der Varianzanalyse oder ANOVA (ANalysis Of VAriance) zum Einsatz. Verfahren wie der Median Test oder der Kruskal-Wallis-Test können zeigen, dass sich die Mittelwerte verschiedener Teilgruppen signifikant voneinander unterscheiden.
Bei diesen Signifikanztests bleibt aber offen, welche Unterschiede im Einzelnen konkret signifikant sind. Mittels Post Hoc Test können wir sowohl verschiedene Paare untersuchen als auch gruppenweise Vergleiche vornehmen, bei denen mehrere Werte zu Gruppen zusammengefasst werden.
Dann lässt sich beispielsweise nicht nur sagen, dass es signifikante Unterschiede zwischen den untersuchten Einheiten gibt, sondern beispielsweise auch, dass die Unterschiede zwischen Gruppe A und B signifikant sind, die zwischen Gruppe B und C aber nicht.
Post Hoc Analyse: Ein Beispiel
Zur Verdeutlichung ein Beispiel: Nehmen wir an, eine Analyse vergleicht die Lebenszufriedenheit in den Städten Berlin, Hamburg, München, Köln, Frankfurt am Main und Leipzig. Ein erster Signifikanztest kommt zu dem grundsätzlichen Ergebnis, dass es signifikante Unterschiede gibt.
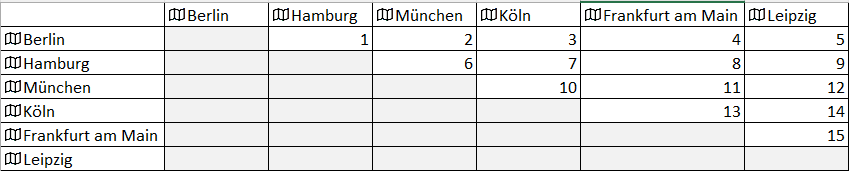
Ein zweiter Test soll nun zeigen, welche Städte sich signifikant voneinander unterscheiden. Da wir sechs Städte untersuchen, gibt es insgesamt 15 verschiedene Paare.
Leipzig lässt sich beispielsweise mit allen fünf anderen Städten vergleichen, Hamburg ausser mit Leipzig noch mit Berlin, München, Köln und Frankfurt, also vier weiteren.
München können wir ausser mit Hamburg und Leipzig noch mit drei weiteren Städten vergleichen, nämlich Berlin, Köln und Frankfurt und so weiter. Am Ende kommen wir auf die oben genannten 15 Paare, sprich: 5 + 4 + 3 + 2 +1 = 15.
Alpha Fehler-Kumulierung vermeiden
Der naheliegendste Gedanke wäre die Prüfung aller einzelnen Verbindungen. Allerdings birgt dies die Gefahr einer sogenannten Alpha-Fehler-Kumulierung. Mit dem Alpha Fehler oder Fehler 1. Art ist gemeint, dass eine Hypothese fälschlicherweise angenommen wird.
Je mehr einzelne Unterschiede getestet werden, desto höher ist die Wahrscheinlichkeit, dass eine Differenz durch Zufall so gross ist, dass sie als signifikant gilt. Mit anderen Worten, selbst wenn es in der Lebenszufriedenheit zwischen den Städten eigentlich keinen Unterschied gibt, könnte es in unseren Daten zufällige Unterschiede geben.
Vielleicht haben wir in einer Stadt besonders viele zufriedene Leute in unserer Stichprobe, in einer anderen besonders viele unzufriedene. Stellen wir uns vor, die Wahrscheinlichkeit, dass ein beobachteter Unterschied zufällig zustande kommt, liegt jeweils knapp unter 5 Prozent. Somit wäre sie signifikant.
Bei 15 Paarungen mit jeweils einer Fehlerquote von unter 5 Prozent haben wir mit mehr als 50 Prozent Wahrscheinlichkeit mindestens einen zufälligen Unterschied.
Post Hoc Test: Die Durchführung
Die Post Hoc Analyse kann die Gefahr einer Alpha Fehler-Kumulierung nicht völlig ausschliessen, sie aber verringern. Der Test auf kleinsten signifikanten Unterschied beruht beispielsweise auf dem Zweistichproben t-Test.
Allerdings wird die Varianz dabei nicht nur auf Basis der beiden untersuchten Gruppen berechnet, sondern auf Basis aller Gruppen. Dadurch liefert er seltener ein signifikantes Ergebnis.
Mit einem Post Hoc Test lassen sich nun nicht nur Unterschiede zwischen einzelnen Werten finden, sondern eben auch Gruppen bilden. In unserem Beispiel könnten wir etwa überlegen, die Städte zu gruppieren, etwa in Gruppen mit hoher und niedriger Lebenszufriedenheit.
Dabei geht es nicht darum, einfach zwei Gruppen aus je drei Städten zu bilden, sondern Gruppen zu finden, innerhalb derer die Unterschiede zwischen den Mittelwerten so klein sind, dass sie eben nicht signifikant sind.
Bei einem üblichen Verfahren werden zunächst alle Werte verglichen, in unserem Fall die Daten für alle sechs Städte. Wenn es einen signifikanten Unterschied gibt, entfernen wir zunächst den obersten Wert und prüfen die Unterschiede erneut. Das gleiche führen wir für den untersten Wert durch.
Im Beispiel würden wir also einmal die fünf Städte mit der höchsten und einmal jene fünf mit der niedrigsten Lebenszufriedenheit untersuchen. Sind die Unterschiede zwischen diesen so gering, dass sie nicht mehr signifikant sind, ist das Vorgehen beendet.
Zu bachten ist freilich, dass bei diesem Verfahren einige Städte zu beiden Gruppen gehören können.
Post Hoc Test: WelcheVerfahren gibt es?
Es gibt zahlreiche Verfahren für den Post Hoc Test. Sie können nach drei wichtigen Kriterien unterschieden werden, nämlich:
- ob Sie Varianzhomogenität voraussetzen,
- ob der Stichprobenumfang gleich sein muss und
- wie konservativ sie sind, ob sie also eher Fehler 1. Art oder Fehler 2. Art begünstigen.
Sind Varianzen und Fallzahl gleich, ist beispielsweise der Ryan-Einot-Gabriel-Welsh Test (REGWF) eine gute Wahl. Bei gleichen Varianzen, aber unterschiedlicher Zahl an Fällen können dagegen der Bonferroni-Test auf kleinsten signifikanten Unterschied der Test von Scheffé eine gute Wahl sein.
Sind Varianzen und Fallzahl ungleich, können Tests auf den kleinsten signifikanten Unterschied oder der Test von Games-Howell eingesetzt werden. Die meisten Tests sind in den üblichen Statistik-Programmen wie SPSS und R enthalten.
Wir sehen: Die Zahl der möglichen Post Hoc Verfahren ist also sehr gross. Hier wird Sie unsere Statistik-Hilfe bei der Entscheidungsfindung gerne unterstützen.
Fazit
Post Hoc Tests gehören zur Gruppe der Signifikanztests. Sie zeigen nicht nur auf, dass es signifikante Unterschiede in den Daten gibt, sondern ermöglicht auch Aussagen darüber, zwischen welchen Gruppen ein Unterschied signifikant ist. Dafür gibt es verschiedene Verfahren, die mit klassischen Statistik-Programmen wie SPSS oder R umgesetzt werden können.