Sogenannte “geclusterte Daten” kommen unter anderem in den Sozialwissenschaften sehr oft vor. Sie können z. B. als Paneldaten oder als Daten mit Mehr-Ebenen-Struktur auftreten. Bei solchen Datensätzen können jedoch Probleme auftreten, die bei einer Analyse zu berücksichtigen sind. Eine praktische Lösung lässt sich aber viel besser festlegen, wenn man die potenziellen Probleme in ihren Grundsätzen versteht. Dies möchten wir mit diesem Beitrag zum Random Intercept Model erleichtern. Und als kleines Extra zeigen wir, wie man mit dem Ganzen gemischten Modellen (Mixed Models) begegnen kann.
Wir unterstützen Sie gerne bei der Aufbereitung Ihrer Daten, der Identifikation möglicherer Fehlerquellen sowie der Auswahl geeigneter Analysemethoden. Wenden Sie sich hierfür an uns für eine professionelle Beratung!
Welche Probleme treten bei geclusterten Daten auf?
Eine zentrale Grundannahme einer (linearen) Regression ist die Unabhängigkeit der Modellfehler oder Residuen. Hierbei handelt es sich um die Abweichungen zwischen den mit dem Modell geschätzten und tatsächlichen Werten der abhängigen Variablen. Das bedeutet, dass die Kenntnis eines Residualwertes keine Möglichkeiten geben darf, einen anderen Residual auch nur in seiner Tendenz vorherzusagen.
“Autokorrelationen” entstehen, wenn sich Beobachtungsfälle hinsichtlich bestimmter Eigenschaften ähneln, die für die Ausprägung der abhängigen Grösse wichtig sind, aber im Modell unberücksichtigt bleiben. Neben der dadurch offensichtlich unvollständigen Erklärung hat dies auch klare technische Konsequenzen. Die Standardfehler werden falsch geschätzt, Konfidenzintervallen und statistischen Tests ist nicht mehr zu trauen. Auch kommt es in solchen Fällen oft zur Überschätzung der Modellgüte (im Sinne von R2).
Am häufigsten tritt dieses Problem bei Zeitreihen auf. Wiederholte abhängige Messungen bilden Cluster von Werten, die tendenziell nach oben oder unten von der mittleren Schätzung abweichen, statt gleichmässig um diese zu streuen. Das Problem ist aber auch bei Daten mit regionalem Bezug oder bei per Design geclusterten Stichproben bekannt. In diesem Fall spricht man oft von einer “Mehr-Ebenen-Datenstruktur”.
Variierende Konstanten oder variierende Effekte? Oder beides?
Ein Beispiel für eine geclusterte Stichprobe: Sie erheben Daten zur Effektivität einer bestimmten experimentellen Lehrmethode. Zehn Schulen erklärten sich bereit, am dazugehörigen Experiment teilzunehmen. Die Schulzugehörigkeit selbst spielt für ihre Forschungsfrage keine Rolle. Das bedeutet jedoch nicht, dass diese in den Analysen ignoriert werden kann.
Es kann sein, dass Schüler*innen in allen zehn Schulen ein unterschiedliches Leistungs-Grundniveau aufweisen. Schüler in einer Schule haben grundsätzlich bessere Noten als in einer anderen. Man spricht dabei von “variierenden Konstanten” oder “Intercepts“.
Möglicherweise zeigt auch die jeweilige Lehrmethode der Schule eine unterschiedliche Wirkung. Die Intervention hat also einen anderen Effekt. Idealerweise passiert dies nicht, aber man weiss nie endgültig, inwiefern sich die untersuchten Fälle in den einzelnen Clustern unterscheiden. In solchen Fällen liegen “variierende Effekte” oder “Slopes“ (Slope wie Steigung, gemeint ist die Steigung der linearen Schätzfunktion) vor.
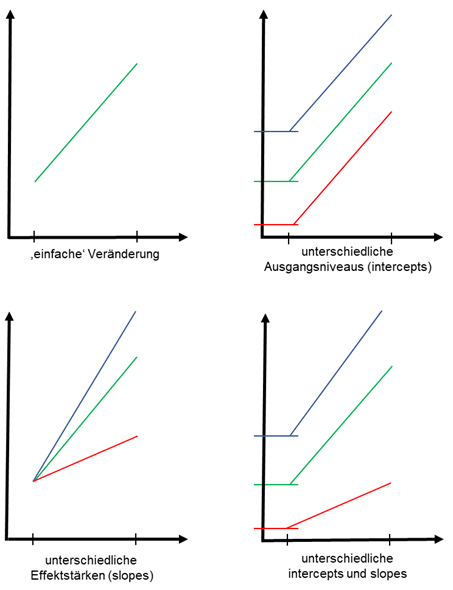
Beide Phänomene können zu nicht vernachlässigbaren Autokorrelation führen, deren Ausmass und Folgen zumindest geprüft werden sollten.
Die Lösung: Mixed Models
Random Intercept Model und Random Slopes Model
In einem früheren Beitrag haben wir bereits die Anwendung von gemischten linearen Modellen bzw. Mixed Models präsentiert. Hierbei können variierende Grundniveaus der abhängigen Variablen und variierende Einflussstärken der unabhängigen Variablen als Random Intecept oder Random Slopes modelliert werden. Dabei werden Zufallsvariablen mit einer gegebenen Verteilungsfunktion (meistens normal) geschätzt und den Werte-Clustern zugewiesen. Diese nennt man “zufällige Effekte”, daher auch die englische Bezeichnung “random“.
Die Ausprägungen dieser Variablen sollte exakt die Abweichungen zwischen den mittleren Parametern und den individuellen Beobachtungen darstellen, die auf die Clusterung in den Daten zurückzuführen sind. Da diese systematischen Abweichungen somit rausgerechnet werden, sind die mittleren Parameter und ihre Tests unverzerrt. Die Berechnung erfolgt dabei explorativ nach dem Prinzip der besten Abbildung der vorliegenden Daten.
Lässt man die Konstante durch eine Zufallsvariable variieren, spricht man von einem Random Intercept Model. Bei variierenden Effekten liegt ein Random Slope Model vor. Es besteht keine Notwendigkeit, Random Intercept und Random Slopes (der unterschiedlichen unabhängigen Variablen) gleichzeitig zu modellieren. Vielmehr soll die Auswahl der Parameter auf Basis des Studiendesigns und der theoretischen Überlegungen über die möglichen plausiblen Verzerrungen erfolgen.
Dummie-Codierung
Im Prinzip kann dasselbe Ergebnis auch ohne zufällige Effekte erreicht werden. Bei variierenden Grundniveaus erfolgt die Berücksichtigung der Clusterzugehörigkeit durch binäre Variablen (Dummies). Für variierende Effektgrössen benötigt man dann zusätzliche Interaktionseffekte zwischen Erklärungsvariablen und diesen Dummies. Diese Methode stösst jedoch bei einer hohen Clusteranzahl und entsprechenden Parametern für die Modellierung schnell an ihre Grenzen. Random Intercept Model oder Random Slope Model sind in diesem Sinne deutlich effizienter.
Bei Mixed Models können die berechneten Zufallsvariablen (meistens dargestellt durch ihre Varianz) zudem dazu genutzt werden, das Ausmass der systematischen Streuung zu überprüfen. Sind die Varianzen von Random Intercept oder Random Slopes nicht signifikant, liegt offensichtlich auch keine Verzerrungen vor. In diesem Fall hätte man ein nachvollziehbares Argument dafür, dass die Grundvoraussetzungen für eine einfache Regression gegeben sind.
Random Intercept Model: Mixed Model in statistischen Programmen
Die gängigen Programme für statistischen Analysen beinhalten Pakete für die Berechnung von Mixed Models, teilweise in mehreren Varianten. Die gängigsten Anwendungen sind hierbei:
- SPSS: MIXED
- R: lme4
- Stata: xtmixed
Wichtig ist, dass in den meisten Fällen für die Berechnung dieser Modelle eine long-Datenstruktur notwendig ist. Daher sollte man gegebenenfalls einige Zeit für die Datenaufbereitung einplanen. Wie das ins SPSS oder Stata gehen kann, haben wir bereits in früheren Beiträgen demonstriert.
Fazit
Random Intercept Model und Random Slope Model sind für die Arbeit mit geclusterten Daten das Mittel der Wahl ─ sei es in Form von Panel- oder Mehr-Ebenen-Daten. Bei einer geschickten Modellierung sind sie anderen verwandten Verfahren in einigen Punkten sogar überlegen. Statistikanfänger*innen haben jedoch oft viel Respekt vor solch ‘fortgeschrittenen’ Methoden. Hinter diesen stehen jedoch relativ einfach nachvollziehbare Annahmen und man sollte deswegen keine Scheu haben, sie in der Praxis anzuwenden.
Falls Sie professionelle Hilfe bei der Auswahl und Anwendung einer passenden statistischen Methode benötigen, erstellen wir Ihnen gerne ein unverbindliches Angebot. Nutzen Sie dazu einfach das schriftliche Kontaktformular!