Die lineare Regressionsanalyse gehört zu den multivariaten Analyseverfahren und erlaubt uns, den Zusammenhang zwischen einer abhängigen Variable und einer oder mehreren unabhängigen Variablen zu analysieren. In diesem Artikel illustrieren wir eine Stata Regression exemplarisch mithilfe von ALLBUS Daten.
Ziel des Artikels ist es zu zeigen, wie wir die relevanten Kennziffern einer Stata Regressionsanalyse interpretieren. Bevor wir uns jedoch der Interpretation einer Stata Regressionsanalyse widmen, werden wir zunächst relevante und zentrale Begrifflichkeiten erläutern.
Sie möchten eine lineare Regressionsanalyse in Stata durchführen und benötigen dafür Unterstützung? Wenden sie sich hierzu an uns und unsere Experten für eine Statistik Beratung!
Abhängige und unabhängige Variable
Die abhängige Variable (AV) einer linearen Regression ist jene, deren Veränderung wir berechnen wollen. In einem Regressionsmodell können wir lediglich eine einzige AV berücksichtigen. Unabhängige Variablen (UV) hingegen sind jene, die die besagte Veränderung der abhängigen Variable bewirken.
Grundsätzlich können mehrere unabhängige Variablen in einem Modell aufgenommen werden: In einem solchen Fall handelt es sich um eine multiple lineare Regression.
Ob eine Variable nun abhängiger oder unabhängiger Natur ist, hängt in erster Linie von der Forschungsfrage ab. Wie eingangs erläutert, erlaubt uns das Verfahren der linearen Regressionsanalyse, den Zusammenhang mehrerer Variablen zu analysieren.
So wäre eine exemplarische Forschungsfrage, welchen Einfluss das Nettohaushaltseinkommen einer Person auf dessen Lebenszufriedenheit hat: Das Nettohaushaltseinkommen wäre in dem Fall die unabhängige Variable; die Lebenszufriedenheit hingegen die abhängige Variable.
Nun könnten wir basierend auf theoretischen Überlegungen argumentieren, dass auch andere Faktoren einen Einfluss auf die Lebenszufriedenheit haben, zB. Alter, Geschlecht, der gesundheitliche Zustand oder der Familienstand einer Person. Auch diese Konzepte könnten wir als AV in der Analyse berücksichtigen.
Unter dieser Prämisse können wir nun diverse Forschungsfragen mithilfe einer Stata Regression beantworten, so wie zum Beispiel:
- Welchen Einfluss hat Rauchen (UV) auf die Fertilität einer Frau (AV)?
- Welchen Einfluss hat die Sprache, die im Familienhaushalt gesprochen wird (UV) auf den Schulerfolg eines Kindes (AV)?
- Unterscheiden sich Männer und Frauen (Geschlecht als UV) hinsichtlich ihrer Statistikfähigkeiten (AV)?
Stata Regression: Ein Beispiel
Kommen wir nun zum Beispiel zur Datenanalyse mit Stata, das wir in diesem Artikel mithilfe von in Deutschland erhobenen ALLBUS-Daten diskutieren werden. Es geht um die Frage, welche Faktoren das Vertrauen in den Deutschen Bundestag beeinflussen.
Dabei wollen wir den Effekt von fünf unabhängigen Variablen analysieren, konkret: Geschlecht, Alter, Bildungshintergrund, politische Selbsteinschätzung sowie Bundesland der Befragten.
Vorab werden die Daten zwecks der Veranschaulichung bereinigt, umkodiert und umbenannt. Damit sind die Variablen in der Form, in der sie hier veranschaulicht werden, nicht im ALLBUS-Datensatz zu finden.
Weiters sind ähnlich wie bei einer Regression SPSS folgende Voraussetzungen relevant: Die Beziehung zwischen den Variablen soll linearer Natur sein, die Residuen sollen unabhängig voneinander und normalverteilt sein, es sollen keine Ausreisser vorhanden sein und weder Multikolinearität noch Homoskedastizität vorherrschen. Für unser Beispiel nehmen wir an, dass alle Voraussetzungen einer linearen Regression erfüllt sind.
Im ersten Analyseschritt ist es wichtig, dass wir uns mit dem Skalenniveaus aller Variablen vertraut machen:
- Die AV „Vertrauen in den Bundestag” wurde mit einer siebenstufigen Likert-Skala erhoben. Das bedeutet, dass die Befragten auf einer Skala von 1 bis 7 einordnen sollten, wie sehr sie dem Deutschen Bundestag vertrauen: 1 bedeutet dabei „kein Vertrauen”, 7 entspricht „hohes Vertrauen”.
- Das Geschlecht wird als Dummy-Variable berücksichtigt mit ja/nein-Kodierungen; damit erhalten Frauen die Ausprägung „ja”, also 1 und Männer die Kodierung „0”.
- Das Alter wurde klassischerweise metrisch (numerisch bzw. intervallskaliert) erhoben.
- Der höchste Bildungsabschluss als sozioökonomischer Hintergrund ist ordinal skaliert mit den Ausprägungen „Niedrig”, „Mittel” und „Hoch”.
- Die politische Selbsteinschätzung ist ebenfalls ordinal skaliert mit den Orientierungen „links” bis „rechts”.
- Schliesslich wurde das Bundesland berücksichtigt, in dem die Befragten zum Zeitpunkt der Datenerhebung lebten. In dieser Analyse interessiert uns lediglich der Unterschied zwischen Neuen und Alten Bundesländern, daher wurde jeweils eine entsprechende Dummy-Variable generiert.
Stata Regression: Analyse & Interpretation
Kommen wir nun zur Interpretation der linearen Regression. Eine lineare Stata Regression führen wir mit dem reg-command durch. Das Präfix i. vor den unabhängigen Variablen dient dazu, die entsprechende Variable kategorial zu berücksichtigen; c. hingegen steht vor kontinuierliche Variablen. Der reg-command wird auch ohne jegliches Präfix erkannt, allerdings werden dann alle Variablen per se als kontinuierlich behandelt.
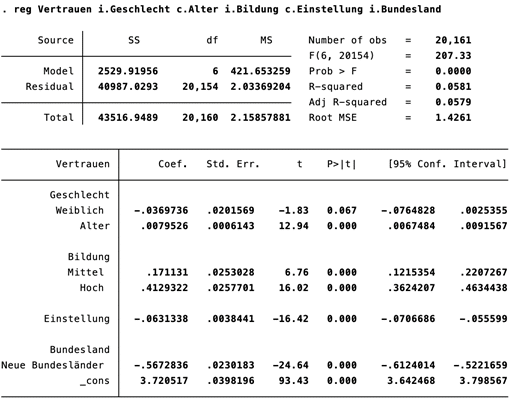
Nun zur Interpretation der Kennziffern: Bevor wir die Koeffizienten der UV betrachten und damit die eigentliche Interpretation der Zusammenhänge, lohnt sich der Blick auf den oberen rechten Kasten des Outputs, der Hinweise zur Güte des Modells gibt.
Von Relevanz ist in diesem Kontext vor allem der der Prob > F Wert, also der p-Wert des gesamten Modells. Als Faustregel gilt, dass p-Werte unter α = 0.05 eine signifikante Erklärungsgüte des Modells abbilden. Dies ist in diesem Fall mit Prob < F = 0.0000 gegeben.
Weiters sind das R-Quadrat beziehungsweise Adjustierte R-Quadrat von Relevanz. Beide Kennziffern sagen aus, wie viel Prozent der Varianz (also der Streuung) der abhängigen Variable durch das Modell erklärt werden. (Das Adjustierte R-Quadrat wird dabei in einer multiplen linearen Regression herangezogen.)
Im vorliegenden Fall beträgt der Wert des Adjustierten R-Quadrat (Adj R-squared) 5.79 Prozent. Das bedeutet, dass das Modell rund 6 Prozent der Varianz des Vertrauens in den Deutschen Bundestag abbildet. Das ist ein vergleichsweise niedriger Wert, allerdings steigt dieser mit der Anzahl der UV, die im Regressionsmodell berücksichtigt werden.
Die Effekte der UV auf die AV “Vertrauen in den Deutschen Bundestag” können wir dem unterem Kasten entnehmen. Als generelle Regel gilt, dass Koeffizienten mit einem positiven Vorzeichen einen positive Beziehung zwischen AV und UV erklären. Ein negatives Vorzeichen steht analog dazu für einen negativen Zusammenhang.
Stata Regression: Einfluss der UV
Wir erinnern uns, dass Geschlecht als Dummy-Variable kodiert und Männern die Ausprägung „0” zugeordnet wurde. Kategoriale Items, zu denen Dummy-Variablen zählen, haben stets eine Referenzkategorie, die im Regressionsmodell nicht sichtbar auftaucht. Stattdessen wird der Effekt der sichtbaren Kategorien (hier: das weibliche Geschlecht) stets im Vergleich zur Referenzkategorie interpretiert. Der Koeffizient für das weibliche Geschlecht beträgt -0.037, zeichnet also einen negativen Effekt auf die abhängige Variable ab.
Konkret ist das Vertrauen in den Deutschen Bundestag unter Frauen um -0.037 Einheiten niedriger als unter Männern. Allerdings ist dieser Effekt nicht signifikant, was wir aus dem p-Wert 0.067 (p > 0.05) ablesen können.
Nun zum Einfluss des Alters: Da die Altersvariable metrisch skaliert ist können wir den Effekt wie folgt interpretieren: Mit jeder Einheit, die das Alter zunimmt (hier: Lebensjahre), steigt das die AV um 0.008 Einheiten. In anderen Worten: Mit steigendem Alter wächst das Vertrauen in den Deutschen Bundestag. Dieser Effekt ist statistisch signifikant, da p < 0.05.
Die Bildungsvariable ist ebenso kategorial skaliert, wobei „niedrige Bildung” als Referenzkategorie dient. Es zeigt sich: Das Vertrauen in den deutschen Bundestag ist unter Personen mit mittlerer Bildung 0.171 Einheiten signifikant höher als unter Personen mit einem niedrigen Bildungsabschluss.
Unter hochgebildeten Personen ist die Diskrepanz noch grösser: Deren Vertrauen in den Deutschen Bundestag ist um 0.413 Einheiten (p < 0.05) höher als jenes der niedrige gebildeten Personen. In anderen Worten: Mit steigender Bildung steigt signifikant das Vertrauen in den Bundestag.
Den Einfluss der politischen Selbsteinschätzung können wir wie folgt interpretieren: Mit jeder Einheit, die sich die Selbsteinschätzung in Richtung „rechts” bewegt, sinkt das Vertrauen in den Deutschen Bundestag signifikante um -0.063 Einheiten (p < 0.05). Es gilt also: Je rechter die politische Selbsteinschätzung der Befragten, desto weniger Vertrauen herrscht vor.
Zuletzt wollen wir Unterschiede zwischen Neuen und Alten Bundesländern interpretieren. Es zeigt, unter Befragten in Neuen Bundesländern herrscht ein niedrigeres Vertrauen in den Deutschen Bundestag vor und im Vergleich zu den Alten Bundesländern ist deren Vertrauen -0.567 Einheiten niedriger. Auch dieser Effekt ist statistisch signifikant mit p < 0.05.
Fazit
In diesem Beitrag haben wir mithilfe von Stata den Output einer multiplen linearen Regression interpretiert. Dabei müssen wir uns vorab unabdingbar mit dem Skalenniveau der jeweiligen Variablen auseinandersetzen, da sich die Interpretation der linearen Regression zwischen kategorialen und kontinuierlichen Variablen unterscheidet.
Ebenso ist die Interpretation der Kennziffern durch der Art der Regression und damit einhergehend durch das Skalenniveau der AV bedingt.Binäre abhängige Variablen finden vor allem in der logistischen Regression Anwendung mit dem Zie, die Wahrscheinlichkeit des Eintreffens eines Ereignisses mithilfe von Koeffizienten (sogenannten Odds Ratio) vorauszusagen.
Für eine professionelle Hilfestellung bei der Auswahl und Anwendung bzw. Interpretation einer Stata Regression zögern Sie nicht und kontaktieren Sie uns! Nutzen Sie dazu gleich und unverbindlich unser schriftliches Kontaktformular!
Weiterführende Links
- ALLBUS 2014 (GESIS Leibniz Institut für Sozialwissenschaften)