Nichtparametrische Tests gelten als Mittel der Wahl, wenn die Normalverteilungsannahme nicht bestätigt werden kann oder eine kleine Stichprobe vorliegt. Dabei bleiben allerdings wertvolle Informationen unbeachtet, eine Einbusse an Trennschärfe oder Power (Teststärke) ist die Folge. Mit Resampling Verfahren stehen aber Verfahren zur Verfügung, die ohne zusätzliche Annahmen die Präzision von Schätzern und Testverfahren verbessern können. Unter dem Begriff Resampling werden dabei verschiedene Verfahren zusammengefasst. Auch die im Data Mining vielfach angewendete Kreuzvalidierung zählt zu den Resampling Verfahren. Im Rahmen dieses Artikels werden zuerst die verschiedenen Testverfahren gegenübergestellt. Anschliessend geben wir eine kurze allgemein verständliche Einführung und Definition von Resampling. Im Weiteren stellen wir verschiedenen Verfahren vor, beispielsweise Bootstrapping Statistik oder Permutation Test.
Gerne beraten wir Sie, welche Verfahren für Ihre Daten oder Fragestellung optimal sind. Wir zeigen Ihnen, mit welchen Verfahren sie die gesamten Informationen Ihren Daten nutzen können. Von einer unverbindlichen Statistik Beratung bis hin zur kompletten Auswertung und Berichterstellung können Sie auf uns zählen.
Folgende Fragen zu Resampling werden in diesem Artikel beantwortet
- Welche Arten von statistischen Testverfahren gibt es?
- Was versteht man unter Resampling Methoden?
- Welche Resampling Methoden werden unterschieden?
- In welchen Situationen bietet sich Bootstrapping Statistik Verfahren an?
- Wie wird ein Permutation Test durchgeführt?
Wer die Wahl hat, hat die Qual: Die Vielfalt der statistischen Testverfahren
Mit einer Erhebung oder Studie soll anhand von Daten beurteilt werden, ob eine Hypothese bestätigt werden kann oder verworfen werden muss. Liegen bereits Informationen über die Variablen vor, beispielsweise über die Verteilungen, so können diese genutzt werden. Bei genügend grosser Fallzahl gelten Verteilungsannahmen oft näherungsweise und können für statistische Testungen genutzt werden. Diese Art der Testung nennt man dann parametrische Tests: Für die Berechnung der Testgrössen werden dabei zusätzliche Informationen über die Verteilung der beteiligten Variablen herangezogen. Durch diese zusätzlichen Informationen ist dann ein Ausschöpfen der gesamten Power einer Studie möglich. Allerdings sind die Testergebnisse auch nur unter der Voraussetzung gültig, dass die getroffenen Annahmen erfüllt sind. Parametrischer Tests sind beispielsweise der t-Test, Gauss-Test, exakter Binomialtest, etc.
Wenn keine Verteilungsannahmen getroffen werden können, stehen nichtparametrische Tests als Alternative zur Verfügung. Die einzige Voraussetzung für die Anwendbarkeit dieser Art der Testung besteht darin, dass die Daten der Grösse nach geordnet werden können. Für die Testung ist also nur relevant, welchen Rang die einzelne Beobachtung einnimmt. Abstände oder Absolutwerte zwischen den Beobachtungen gehen dabei nicht in die Testung ein. Dadurch werden allerdings Informationen ignoriert. Nichtparametrische Tests schöpfen dadurch nicht die gesamte Power aus. Die grössere Anwendbarkeit und das Fehlen jeglicher Annahmen bezahlt man also durch einen Verlust an Power. Nichtparametrische Tests führen deshalb immer zu höheren p-Werten als äquivalente parametrische Tests. Beispiele nichtparametrischer Tests sind Mann-Whitney-U Test, Mediantest, Wilcoxon Test für gepaarte Stichproben,…
Mit zunehmender Verfügbarkeit leistungsstarker Rechner haben sich allerdings vor etwa 25 Jahren die Resampling Verfahren als dritte Säule für den Umgang mit einer kleinen Stichprobe mehr und mehr etabliert. Dabei werden keine Verteilungsannahmen vorab getroffen. Genauso wenig werden asymptotische Aussagen aufgestellt. Somit werden alle Informationen der vorliegenden Stichprobe verwendet.
Was versteht man unter Resampling?
Mit Resampling werden Verfahren bezeichnet, die auf Basis eines vorliegenden Datensatzes wiederholt kleine Stichproben aus diesem Datenpool ziehen. Darauf werden für jede dieser vielen kleinen Stichproben jeweils Populationskenngrössen wie Mittelwert, Standardabweichung, Median, etc. geschätzt. Anschliessend werden die vielen Schätzungen wieder zu einer Masszahl zusammengefasst z. B. durch Mittelwertbildung. Aber auch eine Quantifizierung der Genauigkeit oder Variabilität der Kenngrösse an sich sind möglich, falls die Varianz oder Standardabweichung der vielen Einzelschätzungen berechnet wird.
| Grundgesamtheit | ➜ | Stichprobe | ➜ | Resampling der Stichprobe | ||||||
| x x x
x x x x x x x x x x x x x x x xx x x x x x x x x x x x x x x x x x | R1 | R2 | R3 | R4 | R5 | R6 | ||||
| X1 | X1 | X1 | X1 | X1 | X1 | |||||
| X2 | X2 | X2 | X2 | X2 | ||||||
| X3 | X3 | X3 | X3 | X3 | X3 | |||||
| X4 | X4 | X4 | X4 | X4 | X4 | |||||
| X5 | X5 | X5 | X5 | X5 | ||||||
| X6 | X6 | X6 | X6 | X6 | X6 | |||||
| X7 | X7 | X7 | X7 | X7 | ||||||
| X8 | X8 | X8 | X8 | X8 | X8 | |||||
| X9 | X9 | X9 | X9 | X9 | X9 | X9 | ||||
| X10 | X10 | X10 | X10 | X10 | X10 | |||||
| X11 | X11 | X11 | X11 | X11 | X11 | X11 | ||||
| Mittelwert der Stichprobe: | \(\bar{x}\) | \(\bar{x_{1}}\) | \(\bar{x_{2}}\) | \(\bar{x_{3}}\) | \(\bar{x_{4}}\) | \(\bar{x_{5}}\) | \(\bar{x_{6}}\) | |||
| ↓ | ↓ | |||||||||
| Schätzer für Mittelwert der Grundgesamtheit: | \(\bar{x}\) | \(\overline{x_{1},x_{2},…,x_{6}}\) | ||||||||
Die Anzahl möglicher Subsamples steigt mit dem Stichprobenumfang stark an. Da für jedes Subsample die Kenngrösse berechnet wird, zählen Resampling Verfahren zu den computerintensiven Anwendungen.
Resampling – Vielfältige Verfahren
Die verschiedenen Resampling Verfahren unterscheiden sich hauptsächlich dadurch, nach welchen Kriterien die Subsamples gezogen werden. Insgesamt werden dabei vier verschiedene Resampling Methoden unterschieden:
Kreuzvalidierung (Cross Validation, CV)
Bei der k-fachen Kreuzvalidierung wird die Stichprobe in k gleichgrosse Teilmengen zerlegt, wobei für jede Schätzung k-1 Teilmengen verwendet werden.
Jackknife
Hier werden die Subsamples oder Replikationen gebildet, indem jeweils eine Beobachtung weggelassen wird (delete -1). Wenn mehrere (t) Beobachtungen weggelassen werden, dann spricht man von (delete – t) Jackknife.
Bootstrapping
Beim Bootstrapping wird jedes Subsample durch n-maliges Ziehen mit Zurücklegen aus der ursprünglichen Stichprobe generiert. Die Bootstrapping Statistik beruht dabei auf Subsamples, die den gleichen Stichprobenumfang wie die ursprüngliche Stichprobe haben. Allerdings können hier Beobachtungen mehrfach, keinmal oder einmal vorkommen.
Permutation Test
Bei einem Permutation Test wird die gesamte Stichprobe verwendet. Für jedes Subsample wird hierzu die Reihenfolge der Beobachtungen permutiert, d. h. gewechselt. Anschliessend wird ausgezählt, in wie vielen Fällen ein in Richtung der Alternative extremere Verteilung zu sehen ist. Auf diese Weise werden die p-Werte ermittelt.
Wie viel Resampling ist genug?
Die Anzahl der Replikationen im Resampling hängt vom Stichprobenumfang der Ausgangsstichprobe ab. Während es bei einem Stichprobenumfang von 3 insgesamt 10 mögliche Replikationen im Bootstrapping gibt, sind es für eine kleine Stichprobe von 15 Beobachtungen bereits 77,5 Millionen Replikationen, bei n = 20 insgesamt 69 · 109 mögliche Replikationen.
In den wenigsten Fällen ist ein komplettes Resampling möglich. Statistische Software bietet die Möglichkeit die Anzahl der Samples bzw. Zeitlimits für die Berechnung der Bootstrapping Statistik vorzugeben.
Beispiel aus der Novustat Beratungspraxis
Im Rahmen einer Auswertung für einen Kunden aus dem medizinischen Umfeld liegt eine kleine Stichprobe mit einem Stichprobenumfang von 15 Beobachtungen vor. Dabei handelt es sich um Follow-up Langzeitergebnisse nach Organtransplantation. Der primäre Endpunkt dieser Studie ist die Veränderung eines Scores zur Lebenszufriedenheit, der als stetiges Merkmal auf einer Skala von 1 bis 100 vorliegt.
Resampling in der medizinischen Anwendung
Im vorliegenden Fall ist bei einer kleinen Stichprobe von n = 15 keine Überprüfung der Normalverteilung mit statistischen Verfahren sinnvoll und möglich. Asymptotische Argumentationen mit Hilfe des zentralen Grenzwertsatzes sind bei n = 15 ebenfalls aus der Luft gegriffen. Zudem sind die bereits publizierten Ergebnisse hinsichtlich des Messinstruments zur Lebenszufriedenheit uneinheitlich. In einigen Studien wurden bereits nichtparametrische Verfahren angewendet.
Andererseits vernachlässigen nichtparametrische Schätzungen und Testverfahren gänzlich die stetige Natur der Zielvariablen. Feine Differenzen in der Beurteilung der Lebensqualität werden dabei nicht mehr berücksichtigt. Nichtparametrische Verfahren reduzieren schliesslich das stetige Merkmal Lebensqualität auf die Rangfolge (höchste Lebensqualität, zweithöchste Lebensqualität, …, schlechteste Lebensqualität).
Um möglichst viele Informationen des stetigen Merkmals Lebensqualität zu nutzen und auf Verteilungsannahmen zu verzichten wurden Resampling Methoden angewendet, um die Kenngrössen zu Schätzen. Ein Permutation Test wird verwendet, um Unterschiede zwischen Baseline und follow-up Zeitpunkt inferenz-statistisch zu untersuchen.
Schätzung der Masszahlen mit Bootstrapping Statistik
Im Rahmen der Auswertungen wurden alle Berechnungen mit Bootstrapping Verfahren durchgeführt. Um reproduzierbare Ergebnisse zu erhalten, muss zuerst der Startwert für den Zufallszahlengenerator beliebig festgelegt werden.
Die folgende Tabelle zeigt die Bootstrapping Statistik für die Berechnung der mittleren Differenz (Score Lebensqualität) zwischen Baseline und Follow-up.
Deskriptive Statistik für den Zuwachs Score Lebensqualität zwischen Follow-up und Baseline
| Bootstrapa | |||||||
| BCa 95% Konfidenzintervall | |||||||
| Differenz Follow-up – Baseline (LQ-Score) | Statistik | Std.-Fehler | Verzerrung | Std.-Fehler | Unterer Wert | Oberer Wert | |
| Mittelwert | 48,33 | 4,52 | -,0086 | 4,37 | 40,07 | 56,67 | |
| 95% Konfidenzintervall des Mittelwerts | Untergrenze | 38,63 | |||||
| Obergrenze | 58,04 | ||||||
| Median | 42,00 | 5,50 | 9,98 | 36,00 | 63,00 | ||
a Sofern nicht anders angegeben, beruhen die Bootstrap-Ergebnisse auf 10000 Bootstrap-Stichproben
Anhand der Tabelle kann man ablesen, dass im Mittel über alle Beobachtungseinheiten ein Zuwachs von 48,33 (Standardfehler 4,52) Scorepunkten im Laufe der Beobachtungszeit erfolgte. Im klassischen Fall wird das 95% Konfidenzintervall für den Mittelwert mithilfe der Normalverteilung angegeben als
Mittelwert +/- 97,5 % Quantil der Standardnormalverteilung · Standardfehler =
Mittelwert +/- 1,96 · Standardfehler
Das 95%-Konfidenzintervall ergibt sich im Beispiel als [38,63; 58,04].
Führt man Bootstrapping durch, dann schätzt man die Konfidenzintervalle für den Mittelwert ohne Verwendung der Normalverteilungs-Quantile aus den Daten. Im Beispiel wurden dazu 10000 Bootstrap Stichproben erzeugt. Anschliessend wird im Hintergrund für jede dieser 10000 Stichproben der Mittelwert berechnet. Das Konfidenzintervall ergibt sich dabei als der Bereich, in dem die mittleren 95 % der Mittelwerte aus den 10000 Stichproben sich befinden. Die Bootstrapping Statistik für das 95 % Konfidenzintervall des Mittelwertes beträgt [40,07; 56,67].
Hier ist das Bootstrapping Intervall enger als das parametrische Konfidenzintervall, das auf die Annahme normalverteilter Mittelwerte zurückgreift. Das klassische nichtparametrische Verfahren verwendet anstatt des Mittelwertes den Median als Masszahl für die mittlere Tendenz. Der Median liegt mit einem Wert von 42 deutlich unter dem arithmetischen Mittel.
Permutation Test – Testen ohne Normalverteilung
Im nächsten Schritt soll statistisch untersucht werden, ob der Zuwachs an Lebensqualität (Follow-up – Baseline) signifikant höher als 40 Scorepunkte ist. Das einseitige Signifikanzniveau beträgt 5%.
Dazu soll ein Permutation Test verwendet werden.
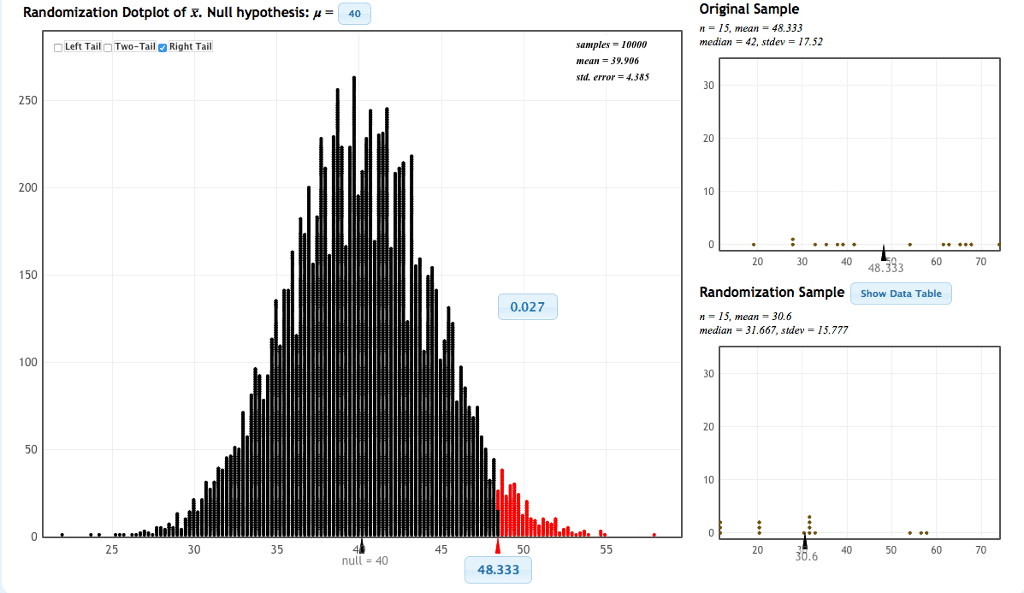
Im rechten oberen Fenster sind die Daten der Studienteilnehmer zu sehen. Das grosse Fenster in der Mitte zeigt dagegen die Häufigkeitsverteilung der Mittelwerte der 10000 Permutationen der Stichprobe. Der in der Stichprobe beobachtete Mittelwert von 48,333 Scorepunkten ist auf der Abszisse markiert. Einen Mittelwert von 48,3333 oder einen noch grösseren Mittelwert hatten nur 0,027 = 2,7 % der Permutationen. Da 2,7 % kleiner ist als das Signifikanzniveau α = 5 %, kann man die Nullhypothese ablehnen. Es kann nachgewiesen werden, dass sich der mittlere Scorewert während der Beobachtungsphase um mehr als 40 Scorepunkte erhöht hat.
Zum Vergleich: Bei parametrischer Testung mit t-Test ergibt sich ein einseitiger p-Wert von 0,0434 und führt somit zum gleichen Ergebnis: Ablehnung der Nullhypothese. Der nichtparametrische Median-Test ergibt in dieser Testsituation einen einseitigen p-Wert von 0,0545 und kann die Nullhypothese nicht ablehnen.
Zusammenfassung
Resampling Verfahren können in bestimmten Situation den Standardverfahren deutlich überlegen sein. Insbesondere eine kleine Stichprobe, eine stetige Zielvariable oder Zweifel an Verteilungsannahmen profitieren von Resampling Verfahren wie Bootstrapping Statistik, Jackknife, Kreuzvalidierung und Permutation Test. Am Beispiel aus der Novustat Beratungspraxis erkennt man, das Bootstrapping Verfahren deutlich mehr aus den Daten herausholen können als beispielsweise nichtparametrische Verfahren, ohne auf fragwürdige Verteilungsannahmen zurückgreifen zu müssen.
Um zu entdecken, welche Möglichkeiten in Ihren Daten stecken, nutzen Sie unsere individuellen Beratung. Nehmen Sie hierzu Kontakt mit uns auf! Wir freuen uns auf Ihr Projekt!
Weiterführende Quellen und Literatur
Das Standardwerk: B. Efron, R.G. Tibshirani: An Introduction to the Bootstrap.
