In vielen Anwendungsbereichen kann man die interessierenden Grössen nicht direkt messen. Beispiele für eine solche sogenannte latente Variable sind Zufriedenheit, Kaufinteresse, Stress, Angst oder Beliebtheit einer Webseite (z.B. bei Web Analytics). Diese Konstrukte werden dann meist anhand verschiedener einzelner Aspekte (Items) erhoben. Die Beliebtheit eines Produkts kann man beispielsweise bei einer Webseitenoptimierung anhand der Selbstbeurteilung, Fremdbeurteilung, Anzahl gekaufter Waren, Verweildauern etc. beurteilen. Diese Art der Darstellung einer Variable durch mehrere andere messbare Variable erfordert allerdings ein methodisch adäquates Modell. Mit einem Strukturgleichungsmodell steht eine flexible und globale Struktur zur Beschreibung solcher Zusammenhänge zur Verfügung. Gegenüber einem linearen Modell kann man sowohl nicht messbare Grössen (latente Variable) als auch manifeste Variablen berücksichtigen.
Im Folgenden geben wir eine verständliche Einführung in die Modellierung mit einem Strukturgleichungsmodell. Wir zeigen dabei, wie mit einem Pfaddiagramm komplexe Zusammenhänge beschrieben werden.
Für tiefergreifende Fragen stehen Ihnen unsere Statistiker gerne zur Verfügung. Gerne beraten wir Sie unverbindlich, wie Ihre Daten ausgewertet werden können und welche Art der Modellierung angewendet werden kann. Nehmen Sie Kontaktformular oder rufen Sie uns an. Wir freuen uns auf Ihre Fragestellung!
Dieser Artikel beantwortet folgenden Fragen:
- Was versteht man unter einem Strukturgleichungsmodell?
- Was sind latente Faktoren?
- Wie geht man bei der Analyse vor?
- Was ist eine Pfadanalyse?
- Wie führt man eine Auswertung durch?
- Wie kann man eine Pfadanalyse in der Praxis anwenden (Anwendungsbeispiel: Webseiteneffektivität)?
Was ist ein Strukturgleichungsmodell?
Ein Strukturgleichungsmodell stellt wie das lineare Modell oder das logistische Modell einen Ansatz dar, um komplexe Zusammenhänge zwischen verschiedenen Grössen zu beschreiben und darzustellen. Das Besondere an dieser Art der Modellierung ist, dass:
- Variablen eingeschlossen werden können, die nicht direkt gemessen werden können (sog. latente Variablen),
- Variablen sich gegenseitig beeinflussen können (Ursache-Wirkung, Kausalität) und
- Messfehler berücksichtigt werden können.
Der Begriff Strukturgleichungsmodell bezeichnet verschiedene Analyseverfahren, die diese Situationen modellieren können, z.B. konfirmatorische Faktoranalyse (CFA), Pfadanalyse, Latente Wachstumskurvenmodelle (latent growth modeling) oder Partial Least Squares (PLS). Das theoretische Konzept hierzu ist sehr komplex. Die Auswertung benötigt ausserdem spezialisierte Softwarepakete wie AMOS, LISREL oder Mplus.
Bestandteile für ein Strukturgleichungsmodell
Im Strukturgleichungsmodell unterscheidet man verschiedene Arten von Variablen:
Indikator (Item oder manifeste Variable)
Ein Indikator ist eine messbare, beobachtbare Variable. Indikatoren können dabei stetig oder kategorial sein. Mithilfe festgelegter Indikatoren wird jede latente Variable geschätzt. Dabei dient ein Indikator zur Schätzung von genau einer latenten Variable. Ein Indikator wird auch als manifeste Variable bezeichnet.
Latente Variable
Eine latente Variable kann nicht direkt erhoben werden. Um eine latente Variable zu schätzen, verwendet man daher mehrere manifeste Variablen (Indikatoren). Wie im linearen Modell sind latente Variablen stetig. Eine latente Variable kann wiederum eine andere Variable beeinflussen. Latente Variablen, die andere latente Variablen beeinflussen, nennt man exogene latente Variablen. Endogene latente Variablen dagegen werden von latenten Variablen beeinflusst.
Für die Beschreibung der Zusammenhänge zwischen den Variablen verwendet man Modelle:
Messmodell
Das Messmodell beschreibt den Zusammenhang zwischen den Indikatoren und den latenten Variablen.
Strukturmodell
Das Strukturmodell modelliert die Beziehungen der latenten Variablen untereinander.
Die Pfadanalyse zur Beschreibung der Zusammenhänge
Die kausalen bzw. strukturellen Beziehungen der Variablen untereinander müssen spezifiziert werden. Dabei stellt die Pfadanalyse einen intuitiven Ansatz zur Beschreibung der wechselseitigen Beziehungen (gerichtet oder ungerichtet) dar. Meist kann man mit der Verwendung von einem Pfaddiagramm auf komplizierte mathematische Gleichungssysteme verzichten.
Der kritische Punkt bei der Pfadanalyse ist die Festlegung der kausalen Beziehungen: Welche Variable beeinflusst eine andere? Was wird als Ursache, was als Wirkung angesehen. Diese zentralen Fragen müssen im Rahmen der Pfadanalyse auf Basis sachlogischer Überlegungen geklärt werden.
Übliche Konventionen bei der Erstellung eines Pfaddiagramms
- Eine latente Variable wird als Ellipse dargestellt
- Manifeste Variablen oder Items werden als Rechtecke gezeichnet.
- Pfeile repräsentieren direkte Effekte von einer Variable auf eine andere.
- Linien mit Pfeilen an beiden Enden stellen eine Korrelation zwischen zwei Variablen dar.
Strukturgleichungsmodell Beispiel: Webseitenoptimierung im Rahmen von Web Analytics
Ein Kunde möchte eine Webseitenoptimierung durchführen und herausfinden, wie die Internetpräsenz seines Unternehmens auf Besucher wirkt.
Der Ausgangspunkt für die Modellierung ist dabei die Hypothese: Nützlichkeit und Inspiration führen zu einer hohen Zufriedenheit der Kunden.
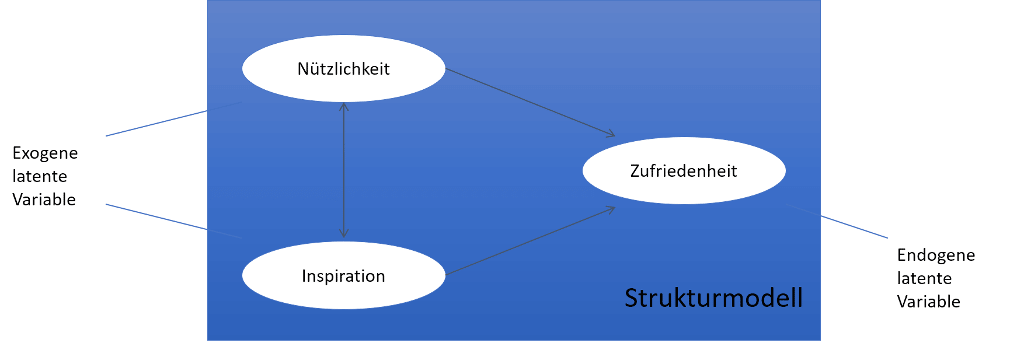
Strukturmodell
Das Strukturmodell bildet die Beziehungen zwischen den latenten Variablen ab. Zufriedenheit stellt eine endogene latente Variable dar. Nützlichkeit und Inspiration sind exogene latente Variablen, da diese auf die Zufriedenheit wirken.
Messmodell der exogenen latenten Variablen
Nützlichkeit und Inspiration der Webseitenbesucher können nicht direkt gemessen werden. Sowohl Inspiration als auch die Beurteilung der Nützlichkeit hängen von vielen Faktoren ab. Im Rahmen eines Fragebogens, den Webseitenbesucher vor Verlassen der Unternehmensseiten ausfüllen konnten, wurden verschiedene Aspekte dieser Konstrukte für die Webseitenoptimierung erfragt. Zudem stehen Daten der Web Analytics Tools zur Verfügung, z. B. Häufigkeit der Besuche, Verweildauer, Vorgänger-, Nachfolger-Seiten etc.
Inspiration wird über die Items Beurteilung der Webseitenbilder, gegenwärtige Stimmungslage, Freude auf Produkt beschrieben. Für die Nützlichkeit werden dagegen die Indikatoren Anzahl aufgerufener Unternehmensseiten, verbrachte Zeit auf Unternehmensseiten, Schwierigkeiten im Ablauf und Bewertung der Übersichtlichkeit herangezogen.
Dies führt also zu folgenden Messmodell der exogenen latenten Variablen:
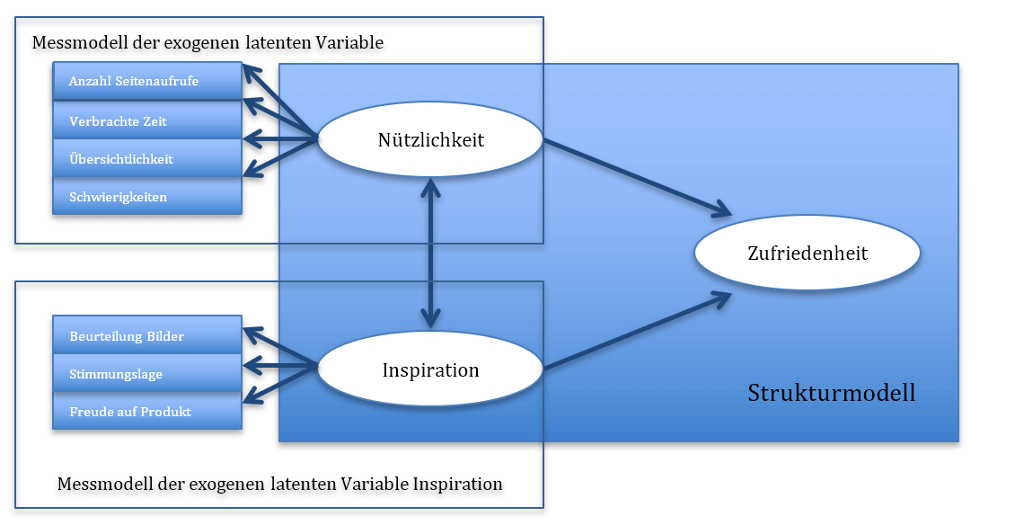
Messmodell der endogenen latenten Variablen
Die latente endogene Variable Zufriedenheit kann nur indirekt beobachtet werden. In diesem Beispiel wird die Zufriedenheit der Webseitenbesucher deshalb über Kaufabwicklung, Anzahl gekaufter Artikel und Weiterempfehlung ausgedrückt. Somit können wir auch für die Zufriedenheit ein Messmodell ergänzen:
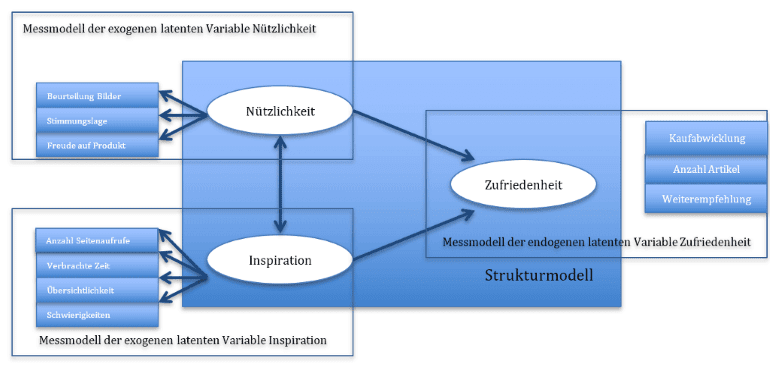
Die Gesamtheit der Messmodelle und des Strukturmodells wird dabei als vollständiges Strukturgleichungsmodell bezeichnet.
Strukturgleichungsmodell als Kausalmodell
Obwohl Strukturgleichungsmodelle oft als Kausalmodell bezeichnet werden, können keine Ursache-Wirkung Zusammenhänge überprüft werden. Mit einem Strukturgleichungsmodell lässt sich also nicht nachweisen, dass die Zufriedenheit eine Folge von Nützlichkeit und Inspiration ist. Der Name Kausalmodell erklärt sich dadurch, dass vom Anwender kausale Beziehungen der latenten Variablen explizit festgelegt werden müssen. Dafür können zeitliche Aspekte sowie sachlogische Überlegungen Entscheidungshilfen darstellen.
Voraussetzung Strukturgleichungsmodell
Um ein Strukturgleichungsmodell anwenden zu können, müssen folgende Voraussetzungen erfüllt sein:
- Lineare Zusammenhänge zwischen den Variablen. Jede durch einen Pfeil dargestellte Beziehung wird üblicherweise mit einem linearen Modell geschätzt.
- Multinormalverteilung
- Anzahl bekannter Parameter übersteigt die Anzahl unbekannter Parameter, d. h. genügend viele Indikatoren zur Festlegung der latenten Variablen. Keine inflationäre Verwendung latenter Variablen.
- Genügend grosser Stichprobenumfang
Vorgehensweise zur Parameterschätzung
Ein Strukturgleichungsmodell wird in mehreren Schritten untersucht.
- Formulierung der Hypothesen
- Bestimmung der latenten Variablen zur Beschreibung der Hypothese
- Auswahl messbarer manifester Variablen für alle latenten Variablen
- Erstellung eines Pfaddiagramms und Spezifikation der Modellstruktur
- Schätzung der Parameter und statistische Testung der Parameter
- Modellanpassung
- Interpretation
Durchführung einer Analyse eines Strukturgleichungsmodells
Strukturgleichungsmodelle kann man mit vielen gängigen Statistikprogrammen analysieren. Amos, MPlus und Lisrel sind kommerzielle Produkte, die speziell auf Strukturgleichungsmodelle ausgerichtet sind. Für R stehen dagegen mit den Packages SEM, lavaan oder semPLS viele open-source Möglichkeiten zur Verfügung. Eine gewinnbringende und effektive Modellbildung erfordert allerdings ein hohes Mass an Expertise und Erfahrung. Besonders die Modellerstellung und Spezifikation der kausalen Beziehungen, die Messung der manifesten Variablen, die Fragebogenerstellung sowie der Interpretation der Ergebnisse sind anspruchsvolle und sensible Aufgabenbereiche. Gerne unterstützen wir Sie bei der Modellierung sowie Ihrer Webseitenoptimierung und stehen Ihnen mit unseren Experten zur Seite. Nehmen Sie Kontakt mit uns auf. Wir helfen Ihnen schnell und kompetent.
Zusammenfassung
Das Strukturgleichungsmodell bietet eine flexible Modellierung komplexer Zusammenhänge. Am Beispiel Webseitenoptimierung mit Daten aus dem Bereich Web Analytics haben wir eine aktuelle Anwendung von einem Strukturgleichungmodell vorgeführt. Neben Interaktionen kann z.B. auch eine latente Variable, Messfehler sowie Korrelationen der latenten Variablen untereinander berücksichtigt werden. Die Darstellung mit einem Pfaddiagramm bietet dabei für den Anwender einen intuitiven Zugang zur Beschreibung der Strukturen. Die Schätzverfahren hierzu sind allerdings sehr komplex. Für die Analyse benötigt man daher meistens statistische Softwarepakete. Gleichwohl ist für die Festlegung geeigneter Verfahren, Sicherstellung korrekt gewählter Parameter und v. a. der Interpretation der Ergebnisse die Expertise erfahrener Statistiker unumgänglich. Wir unterstützen Sie hierzu gerne: schnell, unkompliziert, anwendungsbezogen und verständlich. Wir freuen uns auf Ihre Herausforderung!
