Mit einer Studie soll anhand von Daten beurteilt werden, ob eine Hypothese bestätigt werden kann oder verworfen werden muss. Um einen Effekt nachzuweisen, müssen allerdings ausreichend viele Daten vorliegen. Andererseits zieht ein zu hoher Stichprobenumfang eine Studie erheblich in die Länge und bindet Ressourcen. Dies sind also gute Gründe, um sich vorab im Rahmen der Fallzahlplanung und Fallzahlberechnung (auch a priori Poweranalyse) Gedanken um den notwendigen Stichprobenumfang zu machen. Im Nachhinein stellt dagegen die post hoc Poweranalyse eine Möglichkeit dar statistische Studien zu beurteilen.
Gerne beraten wir Sie, welcher Stichprobenumfang für Ihre Studie optimal ist. Wir übernehmen eine professionelle und unabhängige Fallzahlberechnung. Dabei führen wir eine Fallzahlplanung sowie Poweranalyse in enger Absprache und Zusammenarbeit mit unseren Kunden durch. Nehmen Sie Kontakt mit uns auf und vereinbaren Sie eine kostenlose Erstberatung.
Folgende Fragen werden in diesem Artikel beantwortet
- Warum ist eine Fallzahlplanung essentiell für gute Studien?
- Von welchen Faktoren hängt die Fallzahl ab?
- Woher stammen die Vorinformationen?
- Welcher Unterschied besteht zwischen post hoc Poweranalyse und Fallzahlberechnung?
Warum Fallzahlplanung?
Mit jeder Datenerhebung wird ein Ziel verfolgt: Es soll eine Hypothese statistisch mittels eines statistischen Tests überprüft werden. Liegen dabei zu wenige Daten vor, so kann ein vorhandener Effekt nicht nachgewiesen werden. Der Test wird dann ein nicht signifikantes Ergebnis liefern.
Auf der anderen Seite ist die Datenerhebung allerdings immer mit Zeit und Kosten verbunden. Ein zu hoher Stichprobenumfang führt dazu, dass selbst kleine aber unbedeutende Effekte statistisch signifikant sind.
Ein adäquater Stichprobenumfang stellt sicher, dass:
- ein tatsächlich vorhandener Effekt auch nachgewiesen werden kann.
- mit genügend hoher Sicherheit davon ausgegangen werden kann, dass tatsächlich kein relevanter Effekt existiert, falls in der Studie keine Signifikanz nachgewiesen werden kann.
Erst planen, dann sammeln
Bei einer prospektiven Studie erfolgt die Fallzahlplanung vor Beginn der Datenerhebung. Die Fallzahlberechnung ist ein Teil des Studienprotokolls (a priori Poweranalyse). In klinischen Studien ist die Rechtfertigung des geeigneten Stichprobenumfangs vor der zuständigen Ethikkommission sogar vorgeschrieben. Ist die Datenerhebung dagegen bereits abgeschlossen, kann keine Fallzahlplanung mehr durchgeführt werden. Zu diesem Zeitpunkt ist dann eine nachträgliche (post hoc) Poweranalyse möglich.
Auch in deskriptiven oder retrospektiven Studien sollte vorab genau geplant werden, wie viele Daten gesammelt werden müssen.
Zutaten für die Fallzahlplanung
Für die Fallzahlplanung ist eine enge Zusammenarbeit zwischen Anwender und Statistiker unabdingbar. Für die Fallzahlberechnung müssen Festlegungen zu verschiedenen Aspekten gemacht werden:
Der geeignete statistische Test
In Studien werden meist sehr viele Parameter oder Variablen erhoben. Ziel einer konfirmatorischen Studie ist es beispielsweise, eine Hypothese bezüglich einer Zielvariable mit statistischen Methoden zu bestätigen oder zu verwerfen. Ausschlaggebend für den notwendigen Stichprobenumfang ist dabei dann nur die Zielvariable. Die Fragestellung und die Art der Zielvariable (nominal, ordinal, intervallskaliert) legen dabei einen statistischen Test fest. Die Auswahl des korrekten statistischen Tests können dann professionelle Statistiker sicherstellen. Unsere Experten stehen Ihnen hierzu bei einer Statistik Beratung gerne zur Seite.
Abhängig von der Wahl des statistischen Tests werden aber noch weitere Informationen benötigt.
Der nachzuweisende Effekt
Eine wesentliche Grösse für die Fallzahlplanung ist der nachzuweisende Unterschied. Dabei steht die Frage im Vordergrund, wie hoch der erwartete Unterschied der Zielvariable bezüglich der zu vergleichenden Gruppen ist. Der Unterschied muss so hoch gewählt werden, dass eine praktisch relevante Veränderung gemessen wird. Der nachzuweisende Effekt muss aber auch erreichbar sein. Liegt der in der geplanten Studie erreichte Effekt unter den ursprünglichen Vorstellungen, dann wird der statistische Test den Effekt am Ende nicht nachweisen können.
Die Variabilität der Zielvariable
Der Stichprobenumfang ist weiterhin von der Variabilität der Daten abhängig. Wenn zwischen den zu vergleichenden Gruppen grosse Schwankungen hinsichtlich der Zielvariable zu erwarten sind, benötigt man mehr Beobachtungen, um einen vorgegebene Effekt nachzuweisen. Auch die Frage, ob in den Gruppen gleiche Streuung der Zielvariable angenommen werden kann, ist für Fallzahlberechnung wichtig.
Signifikanzniveau des statistischen Tests
Zur Bestimmung der Fallzahl wird das Signifikanzniveau α vorher festgelegt. Damit ist die Wahrscheinlichkeit bezeichnet, ein statistisch signifikantes Testergebnis zu erhalten, obwohl in Wirklichkeit kein Unterschied besteht. In der Regel beträgt das Signifikanzniveau 5 %. Je nach Fragestellung sind aber auch andere Werte denkbar. Aus der Fragestellung ergibt sich, ob die Testung ein- oder zweiseitig durchgeführt wird.
Power der Studie
In der Planungsphase muss zudem die Power der Studie festgelegt werden. Unter Power einer Studie versteht man die Wahrscheinlichkeit, einen tatsächlich vorhandenen Unterschied mit einem statistischen Test nachzuweisen.
Woher stammen die Zutaten?
Fallzahlplanung ist in hohem Mass interdisziplinär und erfordert daher ein enges Zusammenarbeiten von Statistikern und Anwendern. Je präziser das Vorwissen ist, umso effizienter kann dann die Fallzahlberechnung erfolgen. Die Annahmen bezüglich zu erwartender Effekte oder der Streuung kann zuvor im Rahmen von Pilotstudien abgeklärt werden. Ausserdem sind Literaturrecherchen oder Erfahrungen wichtige Quellen. Gerne stehen Ihnen unsere Experten hierzu zur Seite.
Zusammenhang der einzelnen Parameter
Die einzelnen Parameter beeinflussen in Form von komplexen Formeln den Stichprobenumfang. Für jede Fragestellung und Testung gibt es dabei spezielle Formeln. Ganz allgemein gelten allerdings folgende Zusammenhänge:
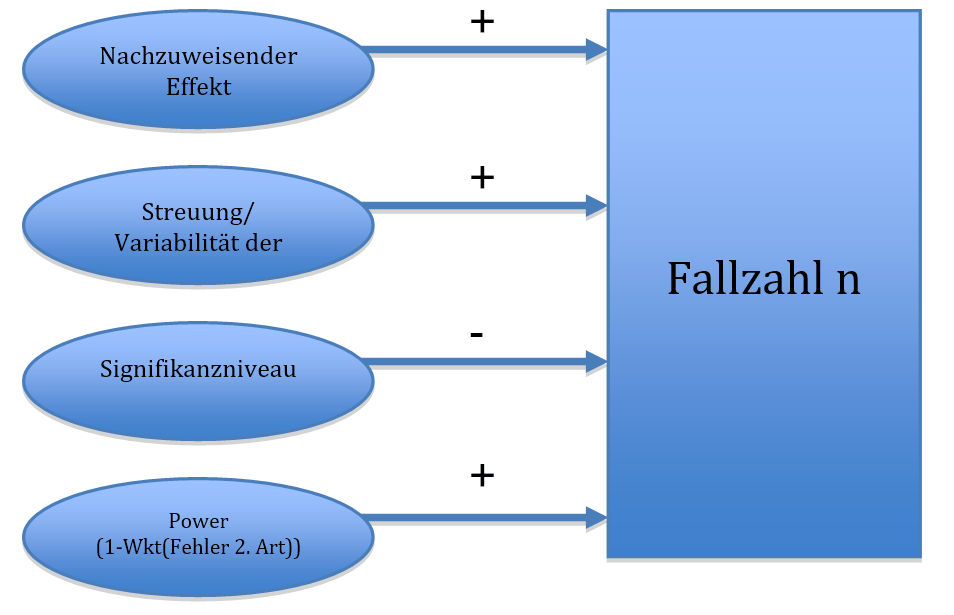
Fallzahlszenarien
Auch mit gewissenhafter Planung und hoher Expertise ist jedoch häufig nur eine grobe Einschätzung der Parameter aus der Zutatenliste möglich. Deshalb werden oft verschiedene Szenarien für festgelegte Intervalle berechnet. So ist es möglich, die Abhängigkeit des Stichprobenumfang von den zu erwartenden Parameterwerten einzuschätzen.
Rezepte wichtiger Fragestellungen
Die obig beschriebenen Zutaten sind allgemein formuliert. Abhängig von der Fragestellung und dem statistischen Test werden für den nachzuweisenden Effekt und die Streuung der Daten zunächst folgende Parameter benötigt. Eine Aufstellung einiger wichtiger Fragestellung ist in der folgenden Tabelle aufgeführt. Darüber hinaus gibt es eine Vielzahl möglicher Modelle und Szenarien. Für eine individuelle Beratung stehen wir Ihnen gerne zur Verfügung.
Ausgewählte Fragestellung und die Parameter für die Fallzahlplanung
| Fragestellung | Stat. Test | Parameter |
| Nachweis eines Unterschieds zweier Gruppen einer stetigen normalverteilten Zielgrösse | t-Test für unverbundene Stichproben | Mittelwert Gruppe 1 Mittelwert Gruppe 2 Standardabweichung Gruppe 1 Standardabweichung Gruppe 2 |
| Vergleich zweier Erfolgswahrscheinlichkeiten/Raten | Exakter Fisher Test | Relative Häufigkeit Gruppe 1 relative Häufigkeit Gruppe 2 |
| Survival Analyse , Vergleich zweier Gruppen | Log-rank Test | Hazardrate Gruppe 1 und Gruppe 2 Zeitfenster Rekrutierung Dauer Follow-up |
| Modellierung einer stetigen Zielvariable in Abhängigkeit von mehreren Einflussvariablen | lineares Modell mit einer Einflussvariable und Kontrollvariablen | Anzahl Kontrollvariablen erwartetes Bestimmtheitsmass R2 bedingtes Bestimmtheitsmass gegeben Kontrollvariablen |
| Logistisches Modell | Baseline Wahrscheinlichkeit Odds ratio Prävalenz |
Weitere Faktoren für Fallzahlplanung
Meist kommt es vor, dass der Stichprobenumfang durch externe Faktoren beschränkt ist. Wenn schon von Beginn an klar ist, dass solche Limitationen eine Rolle spielen werden, kann dies in der Fallzahlplanung Eingang finden. Zeitfenster für die Rekrutierung und Beobachtung von Ereignissen können dann im Rahmen einer Survivalanalyse berücksichtigt werden.
Ein wichtiger Punkt der Planung ist die Drop-out Rate bzw. Lost-to-Follow-up. Darunter versteht man Studienteilnehmer, die vorzeitig abbrechen. Messwerte stehen somit nicht für den gesamten Beobachtungszeitraum zur Verfügung. Ist eine hinreichende Datenerhebung bei einem Teil der Studienteilnehmer nicht möglich, so muss der Stichprobenumfang entsprechend diesem Anteil erhöht werden. Dies gilt auch für Befragungen bei fehlenden Werten, solange diese nicht systematisch erfolgen.
Bei bestimmten Studiendesigns wie z. B. Fall-Kontroll Studien müssen unterschiedliche Fallzahlen in den zu vergleichenden Gruppen berücksichtigt werden. So ist die Anzahl der Fälle oft beschränkt (Prävalenz, Rekrutierungsfenster, etc.).
Werden mehrere (primäre) Endpunkte in einer Studie untersucht, so muss in der Fallzahlplanung sichergestellt werden, dass insgesamt das Signifikanzniveau gehalten wird. Diese Problematik wird als multiples Testproblem bezeichnet.
Post-hoc Poweranalyse
Wenn bereits die Beobachtungen eine Studie vorliegen, so ist im Nachhinein keine Fallzahlplanung oder Fallzahlberechnung mehr möglich. Eine post-hoc Poweranalyse bietet jedoch die Möglichkeit, die Wahrscheinlichkeit für einen Fehler 2. Art bei vorgegebener Fallzahl zu beurteilen.
Aus der Praxis: Fallzahlplanung bei Novustat
Eine Umfrage innerhalb eines Unternehmen soll geplant werden. Ziel der Befragung ist es, die Zufriedenheit von Führungskräften mit der Zufriedenheit von Mitarbeitern ohne leitende Funktion zu vergleichen. Aufgrund der Grösse des Unternehmens ist eine Vollerhebung nicht sinnvoll. Für die Beurteilung der Zufriedenheit wird ein standardisierter Fragebogen verwendet. Die Zielvariable stellt ein Summenscore dar, der in drei Kategorien eingeteilt wird: Unzufriedenheit, Ausgewogenheit sowie Zufriedenheit.
Die Forschungshypothese lautet, dass Mitarbeiter mit Führungsaufgaben zufriedener sind als Mitarbeiter ohne Führungsaufgaben.
Das geeignete statistisches Testverfahren für diese Fragestellung ist der Chi-Quadrat Unabhängigkeitstest. Als Vorinformation wird zunächst die Effektstärke benötigt. Dazu stellte sich im Gespräch mit dem Kunden heraus, dass dieser vorab von folgenden Antworthäufigkeiten in den beiden Mitarbeitergruppen ausgeht: Für die Mitarbeiter ohne Führungsaufgaben wird angenommen, dass 10 % zufrieden, 60 % ausgewogen und 30 % unzufrieden sind. Es wird erwartet, dass sich die diese Häufigkeiten in der Gruppe der Führungskräfte zugunsten höherer Zufriedenheit verändern: 30 % zufrieden, 50 % ausgewogen, 20 % unzufrieden.
Diese Angaben führen zu einer Effektstärke von 0,254. Mit einer Power von 80 % und einem Signifikanzniveau von 5 % werden insgesamt mindestens 150 komplett beantwortete Fragebögen benötigt, also 75 Führungskräfte und 75 Mitarbeiter ohne Führungsaufgaben. Diese Fallzahl ist dabei auf den hohen nachzuweisenden Effekt zurückzuführen.
Erstellung von Fallszenarien für die Poweranalyse
Im Austausch mit dem Kunden wurde mehrere Szenarien untersucht, in denen die Effektstärke variiert wurde. Welche Fallzahl muss man verwenden, wenn der Unterschied zwischen den beiden Mitarbeitergruppen weniger extrem ausfällt?
Ausserdem wurde die Fallzahl untersucht, falls die angestrebte Power von 80 % auf 90 % erhöht wird.
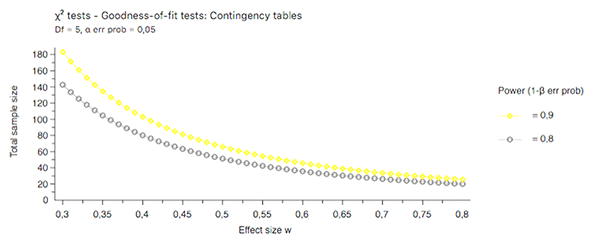
Reduziert man die nachzuweisende Effektgrösse von 0,68 wie ursprünglich angenommen auf einen mittleren Effekt von 0,5, so benötigt man insgesamt mindestens eine Fallzahl von n = 52 bei 80 % Power und n = 66 bei 90 % Power. Effektgrössen im Bereich von 0,3 bis 0,5 gelten beim Chi-Quadrat Anpassungstest als moderate Effekte. Eine weitere Reduzierung des nachzuweisenden Effektes auf 0,3 hat einen deutlichen Anstieg auf n = 143 (Power 80 %) bzw. n = 183 (Power 90 %) zur Folge.
Nach eingehender Diskussion der Szenarien wurde schliesslich eine mittlere nachzuweisende Effektstärke von 0,4 bei einer Power von 80 % als relevant festgelegt. Damit wird eine Fallzahl von mindestens n=81 Fragebögen benötigt, d.h. 41 Mitarbeiter in Führungsposition und 41 Mitarbeiter ohne Führungsaufgaben. Aus vergangenen Befragungen weiss man, dass mit einer Rücklaufquote von 80 % zu rechnen ist. Zudem soll berücksichtigt werden, dass einige Mitarbeiter unvollständige Fragebögen zurück geben. Eine Scorebildung ist somit nicht möglich. Insgesamt werden je Gruppe 55 Mitarbeiter zufällig ausgewählt und Fragebögen an diese ausgeteilt.
Auswirkung der Veränderungen verschiedener Parameter auf die Fallzahl eines Chi-Quadrat Anpassungstests
| Veränderung | Effektstärke | Signifikanz-niveau | Power | Drop-out rate (Ausschlussrate) | Fallzahl (gesamt) |
| Effektstärke | 0,3 | 5 % | 80 % | 20 % | 172 |
| 0,4 | 5 % | 80 % | 20 % | 98 | |
| 0,5 | 5 % | 80 % | 20 % | 63 | |
| 0,6 | 5 % | 80 % | 20 % | 44 | |
| 0,7 | 5 % | 80 % | 20 % | 33 | |
| Signifikanzniveau | 0,4 | 0,1 % | 80 % | 20 % | 184 |
| 0,4 | 1 % | 80 % | 20 % | 145 | |
| 0,4 | 5 % | 80 % | 20 % | 98 | |
| Power | 0,4 | 5 % | 80 % | 20 % | 98 |
| 0,4 | 5 % | 85 % | 20 % | 108 | |
| 0,4 | 5 % | 90 % | 20 % | 124 | |
| Drop-out Rate | 0,4 | 5 % | 80 % | 0 % | 81 |
| 0,4 | 5 % | 80 % | 5 % | 86 | |
| 0,4 | 5 % | 80 % | 10 % | 90 | |
| 0,4 | 5 % | 80 % | 20 % | 98 | |
| 0,4 | 5 % | 80 % | 50 % | 122 |
Zusammenfassung
Vor Durchführung jeder Datenerhebung ist eine Fallzahlplanung und Fallzahlberechnung notwendig, um valide Ergebnisse zu erhalten. Bei klinischen Studien und Tierversuchen ist diese sogar zwingend vorgeschrieben und wird vor Erteilung der Zulassung genau überprüft. Aber auch in allen anderen Anwendungsbereichen spricht eine fehlende Fallzahlplanung für eine schlechte Qualität der Studie oder Umfrage. Bei zu geringen Fallzahlen können vorhandene Effekte nicht nachgewiesen werden. Eine zu hohe Fallzahl führt dagegen zum Nachweis praktisch irrelevant kleiner Effekte und hat hohen Ressourcenverbrauch zur Folge.
Die Fallzahlplanung hängt von der primären Fragestellung und von der geplanten statistischen Auswertungsmethode ab. Dabei sind vorab eine Reihen von Annahmen bezüglich der Parameter zu treffen. Jede Fallzahlplanung ist daher individuell auf die jeweilige Studie zugeschnitten.
Wurde eine Studie bereits durchgeführt, kann keine Fallzahlplanung mehr vorgenommen werden. Hier setzt dann die post-hoc Poweranalyse an.
Jede Fallzahlplanung und Poweranalyse sollte stets in Zusammenarbeit mit fachkundigen Statistikern erfolgen. Unsere Experten stehen ihnen hierzu zur Verfügung. Wir freuen uns, Sie bei der Planung Ihrer Studie zu unterstützen. Nehmen Sie Kontakt mit uns auf!
Weiterführende Quellen:
- Fallzahlplanung in klinischen Studien
- Bock J., Bestimmung des Stichprobenumfangs für biologische Experimente und kontrollierte klinische Studien. Oldenbourg 1998
- Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39, 175-191.
