In vielen statistischen Analysen werden Effekte auf Signifikanz geprüft. So möchte ein Unternehmen beispielsweise wissen, ob das neue Design der Verpackung zu signifikant mehr Käufen des Produktes führt als die alte Verpackung. Dabei sollte man aber nie vergessen, auch die Grösse und Bedeutung des Effektes einzuordnen. Mit anderen Worten: Wir sollten nicht nur die Signifikanz, sondern auch die Effektstärke berechnen. Wenn Verpackung A zu 1 % mehr Käufen führt als Verpackung B, ist dieser Unterschied bei ausreichend grosser Stichprobe vielleicht signifikant. Gleichzeitig ist der Effekt eventuell aber einfach zu klein, um die Kosten für eine neue Verpackung zu rechtfertigen. Signifikanzwerte sagen also noch nichts über die Grösse und Relevanz eines Effektes aus! Wenn man aber Effektstärken berechnen kann wie Cohen’s d, Eta Quadrat oder den Beta Koeffizient, lässt sich die Grösse eines Effektes auf einen Blick ablesen.
Wir wollen deshalb in diesem Artikel anhand einiger Beispiele zeigen, wie man eine Effektstärke berechnen und interpretieren kann. Für eine tiefer gehende Beratung zum Thema statistische Auswertung können Sie jederzeit die Hilfe unserer Experten anfordern!
Dieser Artikel beantwortet folgende Fragen:
- Was ist eine Effektstärke?
- Wie kann man die Effektstärke Cohen’s d berechnen?
- Wofür wird Eta Quadrat eingesetzt und wie kann man diese Effektstärke berechnen?
- Was hat es mit dem Beta Koeffizienten auf sich?
Was ist eine Effektstärke?
Wie der Name schon verrät, gibt die Effektstärke an, wie stark oder bedeutsam der Effekt ist. Es gibt eine Vielzahl an unterschiedlichen Effektstärken (Korrelationskoeffizienten, Cohen’s d, Eta Quadrat, Beta Koeffizient, etc.). Diese Effektstärken eigenen sich für unterschiedliche Anwendungen, haben aber ein paar Eigenschaften gemeinsam:
- Wenn kein Effekt besteht, beträgt die Effektstärke 0
- Umso stärker der Effekt, umso weiter entfernt ist die Effektstärke von 0
- Die Effektstärke ist unabhängig von der Einheit und Skalierung der Daten
- Die Effektstärke ist (anders als der p-Wert und die Signifikanz) unabhängig von der Stichprobengrösse
Die Rolle von Effektgrössen lässt sich allerdings am einfachsten anhand von Beispielen darstellen. Deshalb schauen wir uns zuerst einmal ein Beispiel für Cohen’s d an.
Wohl bekommt’s: Cohen’s d im Geschmackstest
Die Teufelsbräu GmbH vermarktet selbst gebraute Biersorten. Der Braumeister hat vor kurzem eine neue Rezeptur für das Hefeweizen entwickelt, doch der Marketing-Chef der Brauerei ist skeptisch. Er möchte erst eine Geschmackstest-Studie durchführen lassen, bevor die alte Rezeptur ersetzt wird. Ein Mitarbeiter organisiert darauf eine Studie mit sehr grosser Stichprobe. In dieser bewerten Versuchspersonen entweder das Getränk mit der alten oder mit der neuen Rezeptur. Mithilfe eines t-Tests wird daraufhin auf Unterschiede in der Bewertung zwischen den beiden Rezepturen getestet.
Effektstärke: Auf die Skalierung kommt es an!
Nachdem die Studie abgeschlossen ist, fragt der Marketing-Chef nach den Ergebnissen: “Die neue Rezeptur wurde durchschnittlich 2 Punkte besser bewertet als die alte Rezeptur. Ein signifikanter Unterschied”, berichtet ihm sein Mitarbeiter. “Das klingt ja recht ordentlich.” denkt sich der Marketing-Chef. Trotzdem fragt er sicherheitshalber noch einmal nach: “Wie wurde denn der Geschmack genau bewertet?”. “Auf einer Skala von 1 bis 100. Die durchschnittliche Bewertung für die alte Rezeptur war 70. Die Bewertung für die neue Rezeptur war 72.” Das klingt allerdings schon wieder weniger eindrucksvoll. Der Baumeister erhält darum den Auftrag, die neue Rezeptur noch einmal zu überarbeiten.
Die neue Rezeptur wird nach der Überarbeitung schliesslich in einer erneuten Studie noch einmal mit der alten Rezeptur verglichen. Diesmal entscheidet man sich aber für eine Skala von 1 bis 10. Auch in dieser Studie wird die überarbeitete Rezeptur durchschnittlich 2 Punkte besser bewertet als die alte Rezeptur. Die alte Rezeptur wurde im Durchschnitt mit 7 bewertet. Die neue Rezeptur wurde dagegen mit 9/10 Punkten bewertet.
In beiden Studien betrug der absolute Unterschied zwischen den Rezepturen also 2 Punkte in der Bewertung. Ganz offensichtlich war der Effekt der neuen Rezeptur in der zweiten Studie aber wesentlich eindrucksvoller. Die relative Stärke des Effektes unter Berücksichtigung der Skalierung und Einheit der Daten war grösser. Wir können diesen Unterschied deutlich machen, wenn wir die jeweilige Effektstärke berechnen. Für den Vergleich von Mittelwerten von zwei Gruppen können wir Cohen’s d verwenden. Schauen wir uns dazu die Studien einmal genauer an:
| Studie 1 | Studie 2 | |
|---|---|---|
| Mittelwert für die neue Rezeptur | 72 | 9 |
| Mittelwert für die alte Rezeptur | 70 | 7 |
| neue Rezeptur – alte Rezeptur | 2 | 2 |
Effektstärke berechnen mit Cohen’s d
Offensichtlich unterscheiden sich die Studien in Ihrer Skalierung (Studie 1: Bewertung von 1 bis 100, Studie 2: Bewertung von 1 bis 10). Um die relative Effektstärke zu berechnen, müssen wir die Skala aus den Effekten herausrechnen. Diesen Schritt nennt man auch standarisieren und ist häufig notwendig, wenn man die Effektstärke berechnen möchte. Für den Vergleich von Mittelwerten zwischen zwei Gruppen wie hier können wir Cohen’s d verwenden. Cohen’s d rechnet die Skalierung der Daten heraus, indem die Differenz zwischen den Mittelwerten einfach durch die Standardabweichung geteilt wird. In der Regel wird für die Standardabweichung die gepoolte Standardabweichung zusammensetzt, die anhand der Varianz in beiden Gruppen geschätzt wird.:
\(d=\frac{M_{1}-M_{2}}{gepoolte\:Standardabweichung}\) \(=\frac{M_{1}-M_{2}}{\sqrt{\frac{({n_{1}-1})s_{1}^{2}+({n_{2}-1})s_{2}^{2}}{n_{1}+n_{2}-2}}}\)Für unser Beispiel könnten sich zum Beispiel folgende Werte für Cohen’s d ergeben:
| Studie 1 | Studie 2 | |
|---|---|---|
| Mittelwert für die neue Rezeptur | 72 | 9 |
| Mittelwert für die alte Rezeptur | 50 | 70 |
| M(neue Rezeptur) – M(alte Rezeptur) | 2 | 2 |
| gepoolte Standardabweichung | 25 | 2,5 |
| Cohen’s d | \(2/25 = 0,08\) | \(2/2,5 = 0,8\) |
Wie interpretieren wir die berechneten Effektgrössen? Cohen selbst gab folgende Faustregeln an:
| Cohen’s d | Interpretation |
|---|---|
| > 0,2 | Klein |
| > 0,5 | Mittel |
| > 0,8 | Stark |
Wir sehen also, dass der Effekt aus Studie 1 mit Cohen’s d = 0,08 ein sehr kleiner Effekt war. Solche Effekte sind in der Praxis nur selten relevant. Der Effekt der brandneuen überarbeiteten Rezeptur in Studie 2 zeigte dagegen sogar einen grossen Effekt. Solche ein grosser Effekt wäre mit Sicherheit auch von praktischer Relevanz!
Eta Quadrat: Effektstärke berechnen in ANOVA
Wie eingangs erwähnt gibt es eine Vielzahl an unterschiedlichen Effektgrössen für unterschiedliche Anwendungsbereiche. So lässt sich mit Eta Quadrat (oder η²) eine Effektstärke für die Haupteffekte oder Interaktionen in einer ANOVA berechnen. Dabei gibt Eta Quadrat den Anteil der Varianz an, der durch den Effekt erklärt wird. Die Formel für Eta Quadrat lautet:
\(\eta^{2}=Quadratsumme_{Effekt}/Quadratsumme_{Gesamt}\)Die Faustregeln für Eta Quadrat nach Cohen lauten:
| Eta Quadrat | Interpretation |
|---|---|
| > 0,01 | Klein |
| > 0,06 | Mittel |
| > 0,14 | Gross |
Von SPSS wird in der Regel das partielle Eta Quadrat ausgegeben. Dieses ist definiert als das Verhältnis der Varianz vom Effekt zur Varianz vom Effekt zuzüglich Messfehler:
\(partielles\:\eta ^{2}=Quadratsumme_{Effekt}/Quadratsumme_{Effekt}+Quadratsumme_{Fehler}\)Ein Beispiel zur Verdeutlichung:
Die Teufelsbräu GmbH möchte seine neue Rezeptur jetzt in einer aufwendig gestalteten Flasche neu auf den Markt bringen. Nun stehen 4 Designs in der engeren Auswahl. In einer weiteren Studie hat jede Versuchsperson eines der Designs bewertet. In einer ANOVA soll nun geprüft werden, ob es signifikante Unterschiede zwischen den Designs hinsichtlich der Bewertung gibt.
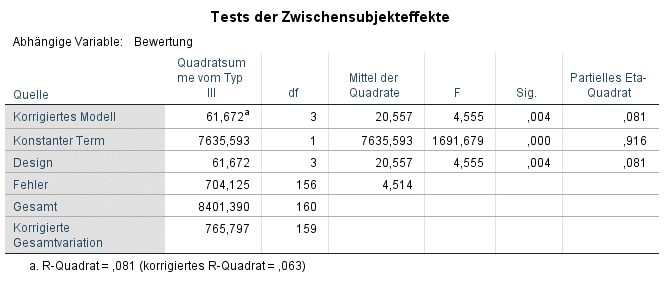
Wie in der Ausgabe zu sehen ist, hatte das Design einen mittelstarken Effekt auf die Bewertung des Produktes, part. Eta-Quadrat = 0,08. Wie genau sich die Designs in der Bewertung unterscheiden kann durch post-hoc Tests geklärt werden.
Beta Koeffizient: Effektstärke berechnen in Regressionsanalysen
Auch in Regressionsanalysen wie der linearen Regression kann man Effektstärken berechnen. Dazu gehören der sogenannte Beta Koeffizient. Die Beta Koeffizienten sind die Regressionskoeffizienten, die man erhalten würde, wenn man die abhängige Variable und alle unabhängigen Variablen in z-Werte umwandeln (standarisieren) würde. Alternativ lassen sich Beta Koeffizienten aber auch aus den normalen unstandarisierten Koeffizienten berechnen:
\(\beta_{j}=b_{j}\cdot \frac{s_{x_{j}}}{s_{y}}\)- \(b_{j}\) bezeichnet den unstandarisierten Regressionskoeffizienten für die unabhängige Variable \(x_{j}\)
- \(s_{x_{j}}\) bezeichnet die Standardabweichung für die unabhängige Variable \(x_{j}\)
- \(s_{y}\) bezeichnet die Standardabweichung für die abhängige Variable \(y\)
Bei einem Beta Koeffizient ist die Grössenordnung vergleichbar mit dem Pearsons Korrelationskoeffizienten r. Für eine einfache Korrelation mit nur einer unabhängigen Variable ist der Beta Koeffizient sogar identisch mit der Korrelation zwischen der abhängigen und unabhängigen Variable. Daher empfehlen wir zur Interpretation die Faustregeln für den Korrelationskoeffizienten r zu verwenden:
| Beta Koeffizient | Interpretation |
|---|---|
| > 0,1 | Klein |
| > 0,3 | Mittel |
| > 0,5 | Gross |
Die Teufelsbräu GmbH möchte in einer weiteren Studie feststellen, welche Faktoren für die Kaufintention Ihrer Produkte eine Rolle spielen. Die Studie wird hierfür als Conjoint Analyse angesetzt. Dazu bewerten Versuchsteilnehmer in verschiedene Produkt-Prototypen der Teufelsbräu GmbH. Die bewerteten Produkte variieren dabei im Preis, Design und Art des Getränks (Weizen oder Pils).
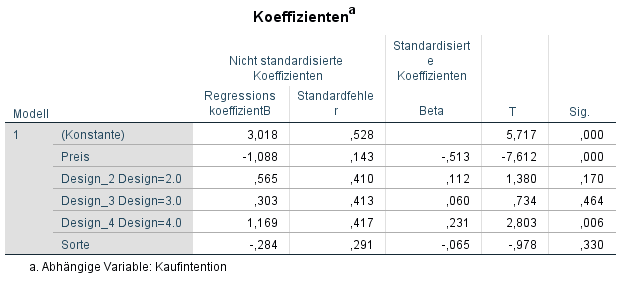
Ein höherer Preis führte zu einer signifikant niedrigeren Kaufintention. Der Beta Koeffizient zeigt, dass es sich hier um einen starken Effekt handelte, β = -0,51. Weiterhin führte Design 4 zu einer signifikant stärkeren Kaufintention als Design 1 (Referenzkategorie). Der Beta Koeffizient zeigt, dass es sich hier um einen eher kleinen Effekt handelte, β = 0,23.
Zusammenfassung
In diesem Artikel haben wir erklärt, was es mit Effektstärken auf sich hat und wie man eine Effektstärke berechnen kann. Dabei sind wir auf drei der am häufigsten verwendeten Effektstärken eingegangen: Cohen’s d, Eta Quadrat und Beta Koeffizient. Wie bereits erläutert gibt es aber noch zahlreiche andere standarisierte Effektgrössen für eine Vielzahl an Anwendungsbereichen. Wenn Sie weitere Unterstützung für Ihre Datenauswertung wünschen, zögern Sie nicht unsere Experten anzufordern!
