Die Spline Regression Anwendung hat sich in der Medizin als eine äusserst effektive statistische Methode etabliert, um komplexe, nichtlineare Zusammenhänge in medizinischen Datensätzen zu modellieren. In der medizinischen Forschung und Praxis sind derartige präzise Modelle und Analysen unverzichtbar.
In diesem Beitrag erfahren Sie, welche Vorteile die Spline Regression und deren Untermethoden, die B-Spline Regression und die Cubic-Regression Spline (kubische Spline Regression), im Vergleich zur linearen Regression bieten.
Was ist die Spline Regression Anwendung?
Die Spline Regression Anwendung ist eine fortschrittliche statistische Methode, die speziell zur Modellierung von nichtlinearen Beziehungen zwischen Variablen entwickelt wurde. Im Gegensatz zur linearen Regression, die sich auf einfache, gerade Linien zur Beschreibung von Datenverläufen beschränkt, nutzt die Spline Regression flexible “stückweise” Polynome, um komplexe Kurven präzise abzubilden. Diese sogenannten „Splines“ sind Abschnitte von Polynomfunktionen, die an definierten Knotenpunkten nahtlos miteinander verbunden werden.
Flexibilität durch Polynome
Der Polynomgrad des Versuchsaufbaus gibt an, wie hoch die höchste Potenz der Variablen in einem Polynom ist. Er bestimmt die Komplexität und Flexibilität des Modells. Höhere Polynomgrade ermöglichen es, komplexere Muster in den Daten zu erfassen. In der medizinischen Datenanalyse werden häufig kubische (Grad 3) Splines verwendet, da sie flexibel genug sind, aber gleichzeitig nicht zu stark oszillieren.
Die Modellanpassung im Versuchsdesign erfolgt jeweils durch die Änderung der Koeffizienten, da diese die Form und den Verlauf der Funktion bestimmen und somit eine bessere Übereinstimmung mit den Daten ermöglichen.
Splines sind besonders wertvoll in der medizinischen Forschung, wo Daten oft nichtlineare und dynamische Muster aufweisen.
Abgrenzung Spline Regression vs. lineare Regression
Demgegenüber ist die lineare Regression eine Methode, die versucht, den Zusammenhang zwischen Variablen durch eine einfache Gerade zu beschreiben. Sie ist geeignet für Daten mit klaren linearen Mustern, stösst jedoch schnell an ihre Grenzen, wenn die Beziehung zwischen den Variablen nichtlinear ist.
| Kriterium | Lineare Regression | Spline Regression |
| Modellkomplexität | Einfache Modellstruktur: beschreibt Daten mit einer einzigen Geraden. | Flexibles Modell: passt sich an Daten mit stückweisen polynomialen Funktionen an. |
| Vorannahmen über Daten | Geht von einem linearen Zusammenhang aus. Beispiel: Der Blutdruck steigt linear mit dem Alter. | Keine strenge Annahme eines linearen Zusammenhangs. Beispiel: Der Blutdruck kann bis zum mittleren Alter steigen und im höheren Alter stagnieren oder sinken. |
| Robustheit gegenüber Ausreissern | Empfindlich gegenüber extremen Werten, die die Gerade verzerren können. Beispiel: Ein Patient mit extrem hohen Blutdruckwerten beeinflusst die Regressionslinie stark. | Weniger anfällig, da die Modellanpassung lokal erfolgt. Beispiel: Ein Ausreisser beeinflusst nur den Spline-Segmentbereich in der Nähe. |
| Glättung | Keine Glättung möglich; modelliert direkt die Datenpunkte. | Kann durch Anpassung der Knotenpunkte und Regularisierung geglättet werden, um Rauschen zu minimieren. |
| Flexibilität bei Modellerweiterungen | Begrenzt, da nur eine Gerade angepasst wird. | Sehr flexibel: Knotenpunkte können hinzugefügt oder verschoben werden, um die Modellanpassung zu optimieren. |
| Einsatz in der medizinischen Forschung | Beschränkt auf einfache Zusammenhänge, wie lineare Dosis-Wirkungs-Beziehungen. Beispiel: Der Medikamenteneffekt steigt mit der Dosis konstant an. | Ideal für nichtlineare Zusammenhänge, zum Beispiel Dosis-Wirkungs-Kurven, die bei bestimmten Dosen einen Plateau-Effekt zeigen. Beispiel: Ein Medikament wirkt nur bis zu einer bestimmten Dosis effizient. |
| Visualisierbarkeit | Einfach zu verstehen und zu visualisieren. Beispiel: Ein 2D-Diagramm mit einer Geraden zur Darstellung des Zusammenhangs zwischen Alter und Cholesterinspiegel. | Komplexer, aber detailreicher: Beispiel: Ein Diagramm, das zeigt, wie der Cholesterinspiegel mit zunehmendem Alter ansteigt, stagniert und dann leicht abnimmt. |
| Optimierungsmöglichkeiten | Kaum optimierbar; basiert nur auf der Berechnung einer Geraden. | Hohe Optimierungsmöglichkeiten durch Auswahl von Knotenpunkten, Spline-Typen (zum Beispiel kubische Splines) und Regularisierung. |
| Übertragbarkeit | Gut auf andere Datensätze übertragbar, solange der Zusammenhang linear bleibt. | Übertragbarkeit hängt von der spezifischen Anpassung an die Daten ab, zum Beispiel der Wahl der Knotenpunkte. |
| Skalierbarkeit bei grossen Datenmengen | Effizient, da geringerer Rechenaufwand. Beispiel: Einfach anwendbar bei 10.000 Patienten. | Kann rechenintensiv sein, wenn viele Knotenpunkte bei grossen Datensätzen erforderlich sind. Beispiel: Analyse von 10.000 Patienten mit detaillierten Wachstumskurven. |
| Flexibilität bei saisonalen Daten | Nicht geeignet, da keine Wiederholungsmuster modelliert werden können. | Ideal für zeitabhängige Daten. Beispiel: Modellierung des saisonalen Auftretens von Grippefällen. |
Erläuterungen
- Modellkomplexität: Die lineare Regression ist deutlich einfacher und leichter verständlich. Die Spline Regression hingegen erfordert mehr Kenntnisse, da sie die Modellstruktur dynamisch anpasst.
- Vorannahmen über Daten: Die lineare Regression setzt voraus, dass der Zusammenhang zwischen den Variablen linear ist, während die Spline Regression diese Annahme aufbricht und sich den Daten anpasst.
- Flexibilität bei saisonalen Daten: Die Spline Regression ist ideal für zeitabhängige medizinische Studien, zum Beispiel bei der Modellierung von Erkrankungsausbrüchen, die saisonal schwanken.
- Skalierbarkeit: Die lineare Regression ist rechnerisch weniger anspruchsvoll und kann problemlos bei grossen Datenmengen eingesetzt werden. Die Spline Regression benötigt jedoch bei komplexeren Modellen mehr Rechenressourcen.
Warum Novustat für Ihre Spline Regression-Projekte?
Die Spline Regression ist insgesamt ein unverzichtbares Werkzeug für die Modellierung komplexer, nichtlinearer Zusammenhänge in der Medizin. Sie ermöglicht, präzise Modelle zur Analyse von Wachstumskurven, Dosis-Wirkungs-Beziehungen und Risikofaktoren zu erstellen.
Novustat bietet Ihnen fundiertes Fachwissen und umfassende Erfahrung in der Anwendung von Spline Regressionen. Unsere massgeschneiderte Beratung unterstützt Sie dabei, das optimale statistische Modell für Ihre spezifischen Anforderungen zu wählen. Mit modernster Software wie R und SPSS gewährleisten wir eine präzise Modellierung Ihrer Daten und liefern Ihnen klar interpretierbare, aussagekräftige Ergebnisse. Senden Sie uns Ihre Anfrage für eine kostenlose Beratung!
Spline Regression Anwendung: typische Situationen
Spline Regression Anwendung – Situation 1: Analyse von Wachstumskurven bei Kindern
- Die Wachstumsentwicklung von Kindern ist ein Paradebeispiel für komplexe, nichtlineare Muster, die mit herkömmlichen linearen Methoden nur unzureichend beschrieben werden können. Während ein Kind in den ersten Lebensjahren schnell wächst, verlangsamt sich das Wachstum typischerweise im späteren Kindesalter, bevor es in der Pubertät erneut zu einem Wachstumsschub kommt.
Warum lineare Regression nicht ausreicht
- Eine lineare Regression würde das Wachstum als gleichmässig steigende Gerade modellieren, beispielsweise indem sie den jährlichen Zuwachs an Körpergrösse konstant hält. Dies vernachlässigt jedoch wichtige Details, wie die unterschiedlichen Wachstumsphasen oder Geschwindigkeitsänderungen über die Jahre hinweg. Als Folge liefert die lineare Regression eine stark vereinfachte und oft unzutreffende Beschreibung der Daten.
Vorteile der Spline Regression
- Mit der Spline Regression können diese komplexen Muster präzise erfasst werden. Sie ermöglicht es, die Daten in verschiedene Intervalle zu unterteilen, wobei innerhalb jedes Intervalls eine separate Wachstumsrate modelliert wird. Übergänge zwischen den Wachstumsphasen werden durch die Knotenpunkte definiert, sodass das Modell den Verlauf glatt und realitätsnah beschreibt. Glatt bezeichnet im statistischen Kontext eine Kurve oder Funktion, die kontinuierlich und differenzierbar ist, sodass sie keine plötzlichen Sprünge oder Knicke aufweist.
Spline Regression Anwendungsfall: Wachstumsphasen
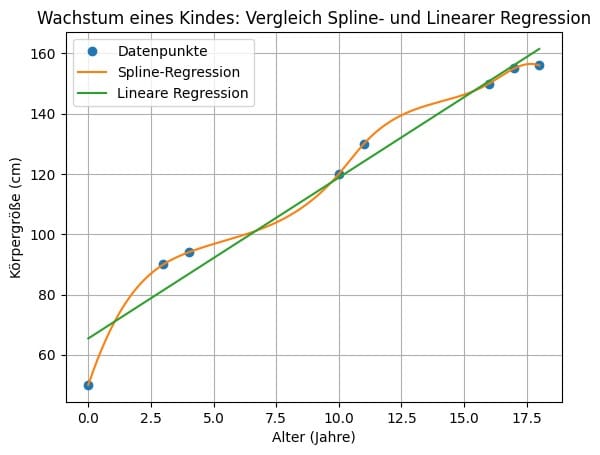
- Angenommen, es wird eine Gruppe von Kindern im Alter von 0 bis 18 Jahren betrachtet. Eine Spline Regression könnte folgende Wachstumsmuster aufzeigen:
- Frühe Kindheit (0–3 Jahre): Sehr schnelles Wachstum, beispielsweise ein Anstieg der Körpergrösse von 50 cm bei der Geburt auf etwa 90 cm mit drei Jahren.
- Kindesalter (4–10 Jahre): Langsameres, aber kontinuierliches Wachstum, etwa 4–6 cm pro Jahr.
- Pubertät (11–16 Jahre): Ein erneuter Wachstumsschub, bei dem die Grösse um bis zu 10 cm pro Jahr zunehmen kann.
- Späte Adoleszenz (17–18 Jahre): Wachstumsstopp oder minimale Zunahme, da die endgültige Körpergrösse nahezu erreicht ist.
Medizinische Relevanz
- Eine detaillierte Modellierung ermöglicht die frühzeitige Erkennung von Wachstumsanomalien, beispielsweise:
- Ausbleiben eines Wachstumsschubs während der Pubertät.
- Ungewöhnlich langsames Wachstum im Vergleich zu Gleichaltrigen.
Spline-Modelle können ferner zur Erstellung von Normkurven verwendet werden, die als Referenz für die Beurteilung des Wachstums einzelner Kinder dienen.
Spline Regression Anwendung – Situation 2: Modellierung von Dosis-Wirkung-Beziehungen bei Medikamenten
Dosis-Wirkungs-Beziehung: Anwendung der Spline Regression
- In der Pharmakologie beschreibt die Dosis-Wirkung-Beziehung, wie sich die Wirkung eines Medikaments in Abhängigkeit von der verabreichten Dosis verändert. Diese Beziehung ist oft komplex und nichtlinear, da verschiedene physiologische Mechanismen in unterschiedlichen Dosisbereichen greifen.
Warum nichtlineare Modellierung erforderlich ist
- Ein typischer Verlauf der Dosis-Wirkungs-Beziehung umfasst:
- Niedrigdosisbereich: Kaum Wirkung, da die Konzentration des Medikaments unterhalb der Wirkschwelle liegt.
- Therapeutischer Bereich: Steigende Dosen führen zu einer deutlichen Zunahme der Wirkung, bis ein Plateau erreicht wird.
- Hochdosisbereich: Bei sehr hohen Dosen können Nebenwirkungen überwiegen, oder die Wirkung nimmt nicht weiter zu.
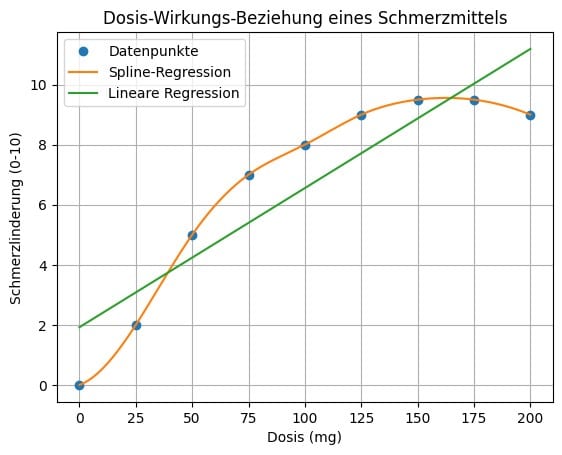
Spline Regression Anwendungsfall: Dosierung Schmerzmittel
- Niedrigdosis (0–50 mg): Keine signifikante Schmerzlinderung, da die Konzentration im Blut zu niedrig ist.
- Mitteldosis (50–150 mg): Schmerzlinderung steigt linear an, da die optimale Dosis erreicht wird.
- Hochdosis (>150 mg): Der Effekt bleibt konstant oder nimmt sogar leicht ab, da die Rezeptoren gesättigt sind oder Nebenwirkungen überwiegen.
- Eine einfache lineare Regression würde die gesamte Dosis-Wirkungs-Kurve als eine einzige Linie darstellen und wichtige Details über- oder unterschätzen. Die Spline Regression hingegen kann Knotenpunkte setzen, zum Beispiel bei 50 mg und 150 mg, um den Verlauf präzise zu erfassen.
Medizinische Relevanz
- Optimale Dosierung: Die Spline Regression ermöglicht die Identifikation der Dosis, bei der die maximale Wirkung ohne signifikante Nebenwirkungen erreicht wird.
- Präzise Modellierung: Sie erfasst nicht nur den Plateau-Effekt, sondern auch abnehmende Wirkungen bei hohen Dosen.
- Patientensicherheit: Eine genauere Analyse hilft, Überdosierungen zu vermeiden und den therapeutischen Bereich einzuhalten.
- Die Spline Regression in der Pharmakologie hilft damit Medikamente sicherer und wirksamer einzusetzen und liefert wertvolle Erkenntnisse für die personalisierte Medizin.
Spline Regression Anwendung – Situation 3: Identifizierung von Risikofaktoren für bestimmte Erkrankungen
Spline Regression in der epidemiologischen Forschung
- In der epidemiologischen Forschung wird die Spline Regression verwendet, um komplexe, nichtlineare Beziehungen zwischen Risikofaktoren und Krankheitsbildern zu modellieren. Im Gegensatz zur linearen Regression, die nur konstante Veränderungen zwischen Variablen annimmt, kann die Spline Regression Schwellenwerte genau abbilden.
Rauchen und Lungenerkrankungen
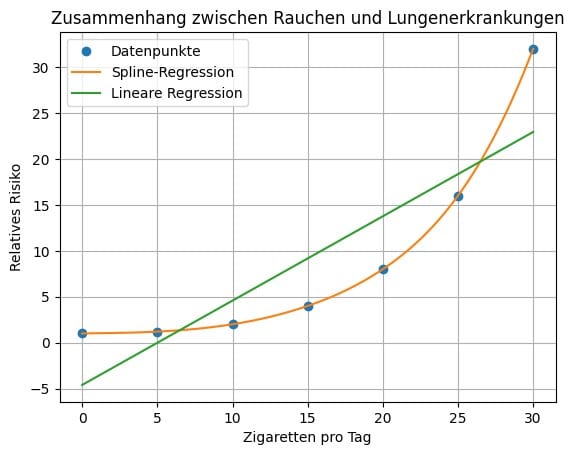
- Ein Beispiel ist der Zusammenhang zwischen Rauchen und der Entwicklung von Lungenerkrankungen. Es wird angenommen, dass das Risiko nicht gleichmässig mit der Anzahl der gerauchten Zigaretten steigt. Stattdessen könnte das Risiko in niedrigen Rauchmengen gering sein und erst ab einer bestimmten Schwelle exponentiell ansteigen.
- Beispielsweise könnte das Spline-Modell zeigen, dass das Risiko für eine Lungenerkrankung bei 10 Zigaretten pro Tag signifikant steigt, während der Unterschied in den ersten 5 Zigaretten pro Tag kaum einen Einfluss hat. Eine lineare Regression würde diese nichtlinearen Muster ignorieren und das Risiko als stetig ansteigend darstellen.
Vorteile der Spline Regression
- Erkennung von Schwellenwerten: Identifikation von Risikofaktoren, bei denen der Einfluss auf die Krankheit ab einem bestimmten Punkt stark zunimmt.
- Komplexe Muster: Modellierung von Beziehungen, die nicht konstant sind, zum Beispiel ein höheres Risiko bei erhöhtem Rauchen, aber auch bei bestimmten altersabhängigen oder geschlechtsspezifischen Unterschieden.
B-Spline Regression und Cubic Regression Splines: Präzision in der Datenanalyse
Die spezialisierte Varianten der Spline Regression, die B-Spline Regression und Cubic Regression Splines, eignen sich besonders für hochkomplexe medizinische Datenanalysen. Beide Varianten bieten gegenüber der „einfachen“ Spline Regression Anwendung erweiterte Möglichkeiten, nichtlineare Beziehungen in medizinischen Datensätzen zu modellieren und ermöglichen eine tiefere Einsicht in vielschichtige Zusammenhänge.
B-Spline Regression: Präzision durch lokale Flexibilität
Die B-Spline Regression arbeitet mit lokal begrenzten Basisfunktionen, die es ermöglichen, komplexe Datenmuster effizient zu modellieren, ohne das gesamte Modell zu beeinflussen. Dies ist besonders hilfreich bei der Analyse hochdimensionaler Daten, wie sie in der genetischen Forschung oder bei der Modellierung von medizinischen Bilddaten vorkommen.
Ein Anwendungsfall ist die Analyse von Genmutationen und deren Einfluss auf Krankheitsrisiken, bei der B-Splines helfen, nichtlineare Zusammenhänge zwischen genetischen Faktoren und der Krankheitsentstehung präzise darzustellen.
Cubic Regression Splines: Glatte Übergänge für Langzeitstudien
Cubic Regression Splines basieren auf kubischen Polynomen, die durch Knotenpunkte miteinander verbunden sind. Diese Technik gewährleistet eine besonders glatte Anpassung an die Daten, was sie ideal für die Analyse von Langzeittrends in der Medizin macht. Ein häufiger Szenario dieser Methode ist die Analyse des Blutzuckerverlaufs bei Diabetikern über mehrere Jahre. Durch die glatte Anpassung an die Daten können präzisere Vorhersagen über den Krankheitsverlauf und die Auswirkungen von Therapieansätzen getroffen werden.
B-Spline Regression vs. Cubic Regression Splines: Unterschiedliche Ergebnisse bei der Blutdruckanalyse
Die unterschiedlichen Ergebnisse der B-Spline Regression und Cubic Regression Splines werden anhand einer Betrachtung des Zusammenhangs zwischen Alter und dem systolischen Blutdruck von Patienten bei einer Blutdruckanalyse deutlich.
- B-Spline Regression: Der Blutdruck könnte in verschiedenen Altersgruppen unterschiedlich stark ansteigen, und B-Splines würden es ermöglichen, diese nichtlinearen Muster präzise zu modellieren. Die Methode kann die Variabilität der Daten besser erfassen, etwa indem sie in jüngeren Jahren einen steileren Anstieg und in älteren Jahren eine Verlangsamung des Anstiegs darstellt.
- Cubic Regression Splines: Diese Methode würde einen kontinuierlichen, aber glatten Verlauf des Blutdrucks über das gesamte Alter hinweg darstellen. Obwohl auch hier die Anstiege und Plateaus erkennbar sind, sorgt die glatte Anpassung der Cubic Splines dafür, dass Übergänge zwischen den verschiedenen Altersbereichen weniger abrupt erscheinen, was besonders bei der Vorhersage von Krankheitsrisiken hilfreich sein kann.
| Kriterium | B-Spline Regression | Cubic Regression Splines |
| Flexibilität | Hohe Flexibilität durch die Verwendung mehrerer lokaler Basisfunktionen, die unterschiedliche Bereiche der Daten abdecken können. | Mässig flexibel, da es nur eine kontinuierliche Anpassung über den gesamten Datensatz bietet, ohne sich stark an lokale Veränderungen anzupassen. |
| Modellstruktur | Verwendet eine Serie von Basisfunktionen, die in lokalen Segmenten wirken, die durch Knotenpunkte miteinander verbunden sind. | Nutzt kubische Polynome, die an Knotenpunkten miteinander verbunden sind, und sorgt so für eine glatte, kontinuierliche Anpassung. |
| Anpassung an Daten | Sehr gut geeignet, um Daten mit abrupten Veränderungen oder stark variierenden Trends zu modellieren. | Bietet eine glatte Anpassung, ideal für Daten, die weniger abrupte Änderungen aufweisen und eher kontinuierliche, stetige Veränderungen darstellen. |
| Anwendung in der Medizin | Besonders vorteilhaft bei der Modellierung von genetischen Risikofaktoren, komplexen biologischen Prozessen oder dynamischen Prozessen mit unterschiedlichen Stadien. | Ideal für die Modellierung von langfristigen, kontinuierlichen medizinischen Prozessen, wie der Blutzuckerentwicklung oder dem Verlauf von Herz-Kreislauf-Erkrankungen. |
| Komplexität der Modellierung | Höhere Modellkomplexität durch zahlreiche Knotenpunkte und potenziell viele Segmente, was zu einer detaillierteren Analyse führt. | Geringere Modellkomplexität, da nur eine begrenzte Anzahl von Knotenpunkten erforderlich ist, aber es könnte weniger präzise auf nichtlineare Muster eingehen. |
| Eignung für nichtlineare Daten | Sehr geeignet für stark nichtlineare Daten, bei denen sich die Beziehung zwischen Variablen abrupt ändern kann. | Geeignet für Daten mit sanften Übergängen und kontinuierlichen Trends, bei denen keine extremen Schwankungen oder Abweichungen erwartet werden. |
| Robustheit gegenüber Ausreissern | Robust gegenüber Ausreissern, da die Anpassung lokal erfolgt und nur in unmittelbaren Bereichen der Daten beeinflusst wird. | Weniger robust gegenüber Ausreissern, da die Anpassung global erfolgt und somit extreme Werte den gesamten Verlauf der Kurve beeinflussen können. |
| Anpassung an saisonale oder zyklische Muster | Sehr gut geeignet, um saisonale oder zyklische Schwankungen zu modellieren, zum Beispiel saisonale Krankheitsmuster. | Kann saisonale Muster modellieren, aber weniger flexibel in Bezug auf unregelmässige Zyklen oder stark wechselnde Trends. |
| Optimierung der Knotensetzung | Hohe Flexibilität bei der Wahl und Platzierung der Knotenpunkte, was die Anpassung an komplexe Datenmuster ermöglicht. | Knotensetzung erfolgt meist an festgelegten Punkten, was weniger Flexibilität bei der Modellanpassung bietet. |
| Berechnungsaufwand | Höherer Rechenaufwand, da eine grössere Anzahl von Knotenpunkten und Basisfunktionen berücksichtigt werden müssen. | Geringerer Rechenaufwand im Vergleich zu B-Splines, da weniger Knotenpunkte benötigt werden. |
| Skalierbarkeit bei grossen Datensätzen | Kann bei sehr grossen Datensätzen ressourcenintensiv werden, insbesondere wenn viele Knotenpunkte erforderlich sind. | Besser skalierbar bei grossen Datensätzen, da die Anzahl der Knotenpunkte oft begrenzt ist und weniger Ressourcen benötigt werden. |
| Visualisierung der Ergebnisse | Kann komplexe, hochauflösende Datenmuster darstellen, jedoch schwieriger zu visualisieren aufgrund der Vielzahl an Knotenpunkten und Segmenten. | Einfacher zu visualisieren aufgrund der kontinuierlichen Anpassung, bietet jedoch möglicherweise weniger Detailgenauigkeit bei komplexen Daten. |
| Anpassung an nicht-uniforme Zeitintervalle | Sehr gut geeignet für Daten mit unregelmässigen Zeitintervallen, wie sie häufig in der klinischen Forschung vorkommen. | Weniger flexibel bei der Modellierung von nicht-uniformen Zeitintervallen, da es eine gleichmässige Verteilung der Knotenpunkte voraussetzt. |
B-Spline Regression oder Cubic Regression Splines?
Die Wahl zwischen B-Spline Regression und Cubic Regression Splines hängt jeweils von den spezifischen Anforderungen der medizinischen Studie und der Art der vorliegenden Daten ab. B-Splines bieten eine höhere Flexibilität und sind besonders bei komplexen, heterogenen Daten von Vorteil, während Cubic Splines für kontinuierliche und langfristige Trendanalysen ideal sind.
Beispiel: Vergleich der vier Regressionsmethoden zur Modellierung des Bluthochdrucks
Es soll der Zusammenhang zwischen dem Alter und dem systolischen Blutdruck mittels der der vier Regressionsmethoden untersucht werden. Die zu untersuchende Gruppe besteht aus 100 Patienten im Alter von 20 bis 80 Jahren.
Basierend auf den bisherigen Erkenntnissen aus der klinischen Forschung ist davon auszugehen, dass der systolische Blutdruck mit zunehmendem Alter tendenziell steigt, aber dass die Veränderungsrate nicht konstant ist. Es gibt Hinweise darauf, dass der Blutdruck ab einem bestimmten Alter stagniert oder sogar sinkt.
Um diese Annahmen zu überprüfen und die Daten korrekt zu modellieren, wenden betrachten wir die vier unterschiedliche Regressionsmethoden: Lineare Regression, Spline Regression, B-Spline Regression und Cube-Regression. Jede Methode hat ihre eigenen Stärken und Schwächen, um die Blutdruckveränderung im Alter präzise darzustellen.
Datenbeschreibung
- Alter der Patienten: 20 bis 80 Jahre.
- Systolischer Blutdruck: Die Daten zeigen, dass der Blutdruck bis zum Alter von 40 Jahren rasch ansteigt, danach langsamer zunimmt und ab etwa 70 Jahren stabil bleibt oder sogar leicht abnimmt.
Regressionsmethoden: Anwendung und Ergebnisse
1. Lineare Regression:
- Modellannahme: In der linearen Regression wird angenommen, dass der systolische Blutdruck in einer konstanten Rate mit dem Alter steigt. Diese Methode modelliert die Beziehung zwischen Alter und Blutdruck als eine gerade Linie.
- Anwendung auf das Beispiel: Der lineare Anstieg des Blutdrucks könnte beispielsweise 0,5 mmHg pro Jahr betragen. Wenn der Blutdruck bei einem Patienten mit 20 Jahren 120 mmHg beträgt, würde er nach 40 Jahren bei 160 mmHg liegen, was einen konstanten Anstieg des Blutdrucks über das gesamte Alter hinweg suggeriert.
2. Spline Regression:
- Modellannahme: Die Spline Regression verwendet stückweise Polynomfunktionen, die es erlauben, den Zusammenhang flexibler zu modellieren. Knotenpunkte werden gesetzt, um den Verlauf der Funktion zu verändern. Diese Methode kann die beschriebene nichtlineare Beziehung besser abbilden, da sie für verschiedene Altersgruppen unterschiedliche Steigungen zulässt.
- Anwendung auf das Beispiel: Mit der Spline Regression können Sie Knotenpunkte bei den Altersspannen 40, 60 und 70 Jahren setzen, um den Blutdruckanstieg bis 40 Jahre schnell, zwischen 40 und 60 Jahren langsamer und nach 60 Jahren nahezu stabil darzustellen. Das Modell würde für einen Patienten mit 60 Jahren beispielsweise einen Blutdruck von 145 mmHg und mit 80 Jahren 147 mmHg schätzen, was auf eine Stagnation nach einem raschen Anstieg hinweist.
3. B-Spline Regression:
- Modellannahme: B-Splines stellen eine Variation der Spline Regression dar, wobei die Anpassung an die Knotenpunkte besonders glatt erfolgt. B-Splines ermöglichen eine noch genauere Modellierung der Daten, indem sie die Übergänge zwischen den verschiedenen Segmenten optimieren und grosse Sprünge in der Kurve vermeiden.
- Anwendung auf das Beispiel: Die B-Spline Regression würde den Verlauf des systolischen Blutdrucks ähnlich wie die Spline Regression modellieren, jedoch mit glatteren Übergängen zwischen den Knotenpunkten. Das Modell könnte für einen Patienten mit 60 Jahren einen Blutdruck von 143 mmHg vorhersagen und für 80 Jahre einen Wert von 144 mmHg, wobei der Übergang zwischen den unterschiedlichen Altersabschnitten präzise dargestellt wird.
4. Cube-Regression (Kubische Spline Regression):
- Modellannahme: Die Cube-Regression verwendet kubische Polynomfunktionen zwischen den Knotenpunkten. Diese Methode ist besonders geeignet, um komplexe, nichtlineare Daten zu modellieren, insbesondere wenn es Hinweise auf eine Veränderung im Trend gibt, wie beispielsweise eine Stabilisierung oder sogar ein Absinken des Blutdrucks im höheren Alter.
- Anwendung auf das Beispiel: In diesem Modell könnte der Blutdruck bei einem 60-jährigen Patienten 140 mmHg betragen, aber ab 70 Jahren könnte ein leichter Rückgang des Blutdrucks erfolgen, beispielsweise auf 138 mmHg. Die Cube-Regression bietet durch die Verwendung kubischer Funktionen eine sehr exakte Modellierung, die auch subtile Veränderungen im Alter berücksichtigt.
Vergleich und Ergebnisse der Regressionsmethoden
| Kriterium | Lineare Regression | Spline Regression | B-Spline Regression | Cube-Regression (Kubische Spline) |
| Modellannahme | Konstanter linearer Anstieg des Blutdrucks. | Flexibler Verlauf mit stückweisen Anpassungen. | Glatte Anpassung zwischen den Knotenpunkten. | Sehr präzise, unter Berücksichtigung von Rückgängen oder Sättigung. |
| Datenanpassung | Einfach, keine Nichtlinearität berücksichtigt. | Flexibel, geeignet für nichtlineare Beziehungen. | Sehr präzise Anpassung mit minimalen Sprüngen. | Sehr komplex, berücksichtigt auch Änderungen in der Trendrichtung. |
| Komplexität der Berechnung | Einfach zu berechnen. | Erfordert Knotenpunktwahl und Modellanpassung. | Höher, da B-Splines berücksichtigt werden. | Höher, benötigt kubische Polynomfunktionen und detaillierte Berechnungen. |
| Anpassung an den Blutdruckverlauf | Modifiziert nur den allgemeinen Trend. | Modelliert unterschiedliche Anstiegsraten je nach Alter. | Sehr genau, vermeidet abrupte Änderungen. | Extrem präzise, zeigt mögliche Rückgänge oder Stabilisierung im hohen Alter. |
| Eignung für medizinische Daten | Geeignet für einfache, lineare Beziehungen. | Sehr gut geeignet für komplexe medizinische Daten, die nichtlinear sind. | Hervorragend geeignet für komplexe Muster mit glatten Übergängen. | Optimal für detaillierte medizinische Daten, die sowohl Anstiege als auch Rückgänge abbilden müssen. |
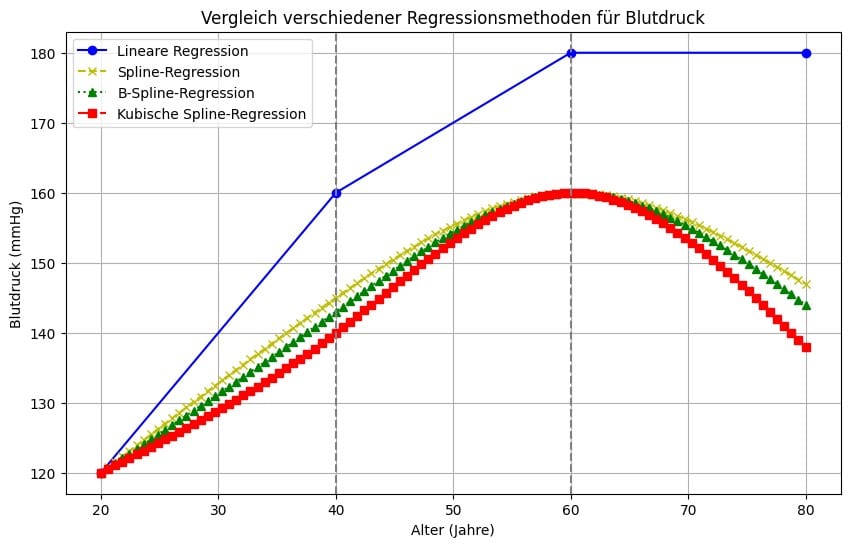
| Beispiel-Blutdruck bei 20 Jahren | 120 mmHg (Ausgangswert) | 120 mmHg (Ausgangswert) | 120 mmHg (Ausgangswert) | 120 mmHg (Ausgangswert) |
| Beispiel-Blutdruck bei 40 Jahren | 160 mmHg (lineare Steigerung) | 145 mmHg (langsamer Anstieg nach 40 Jahren) | 143 mmHg (glatter Übergang) | 140 mmHg (langsamer Anstieg) |
| Beispiel-Blutdruck bei 60 Jahren | 160 mmHg | 145 mmHg | 143 mmHg | 140 mmHg (leichter Rückgang) |
| Beispiel-Blutdruck bei 80 Jahren | 180 mmHg | 147 mmHg | 144 mmHg | 138 mmHg (leichte Rückbildung) |
Interpretation der Ergebnisse
- Lineare Regression: Diese Methode zeigt einen konstanten und direkten Anstieg des Blutdrucks ohne Rücksicht auf spezifische Veränderungen. In der Praxis wäre dieses Modell in den meisten Fällen zu einfach und würde wichtige Details des Blutdruckverlaufs übersehen.
- Spline Regression: Diese Methode ermöglicht es, den Blutdruckverlauf flexibler zu modellieren, insbesondere wenn der Anstieg in verschiedenen Altersgruppen unterschiedlich ist. Sie kann jedoch auch zu ungenauen Vorhersagen führen, wenn die Knotenpunkte nicht optimal gesetzt sind. Dennoch bietet sie eine erheblich bessere Anpassung als die lineare Regression.
- B-Spline Regression: Die B-Spline Regression sorgt für eine noch genauere Anpassung an die Daten, indem sie fliessendere Übergänge zwischen den Knotenpunkten verwendet. Dies macht sie besonders geeignet für die Modellierung von Bluthochdruck, der nicht nur linear ansteigt, sondern auch in den Übergangsphasen verschiedene Verhaltensmuster zeigt.
- Cube-Regression: Mit der Cube-Regression können Sie den Blutdruckverlauf äusserst detailliert modellieren. Diese Methode berücksichtigt sogar die Möglichkeit, dass der Blutdruck ab einem bestimmten Alter nicht nur stagniert, sondern tatsächlich leicht zurückgeht. Das macht diese Methode besonders nützlich für komplexe medizinische Studien, bei denen genaue Vorhersagen des Blutdrucks in späteren Lebensjahren von grosser Bedeutung sind.
Wahl der optimalen Regressionsmethode
Die Präferenz der richtigen Regressionsmethode hängt von der Komplexität der Daten und der spezifischen Forschungsfrage ab. Während die lineare Regression für einfache, lineare Beziehungen ausreicht, bieten Spline- und Cube-Regressionen weit genauere und realistischere Modelle für nichtlineare und komplexe Muster wie den Verlauf des systolischen Blutdrucks über das Alter.
Spline Regression Anwendung: Vergleich R vs. SPSS
Schliesslich ist die Wahl des richtigen Tools zur Durchführung von Spline Regressionen massgeblich, um die vorhandenen Daten bestmöglich auszuwerten. Zwei der beliebtesten Softwarelösungen hierzu in der medizinischen Forschung sind R und SPSS. Beide Programme bieten robuste Methoden für die Spline Regression, doch sie unterscheiden sich in einigen Punkten.
- R ist besonders populär aufgrund seiner Flexibilität und umfangreichen Bibliotheken. Mit Paketen wie „splines“ können komplexe Modelle leicht angepasst und optimiert werden.
- SPSS bietet dagegen eine benutzerfreundliche Oberfläche und ist besonders geeignet für Wissenschaftler, die eine weniger programmiertechnische Herangehensweise bevorzugen.
Unterschiede zwischen R und SPSS bei der Durchführung von Spline Regression
| Kriterium | R | SPSS |
| Flexibilität | Sehr hoch – Bietet vollständige Anpassbarkeit durch Programmierkenntnisse. Ideal für komplexe, benutzerdefinierte Analysen. | Mittel – Einfachere Anpassung, jedoch auf Standardanalysen begrenzt, mit Erweiterungen nur über SPSS-Syntax. |
| Funktionsumfang | Sehr umfangreich – Zahlreiche Pakete und fortgeschrittene Methoden für maschinelles Lernen, Zeitreihen, Bioinformatik. | Eingeschränkt – Gut für Standardanalysen wie t-Tests, ANOVA und Regressionsanalysen, jedoch begrenzt bei spezialisierten Methoden. |
| Anwendungsgebiete | Breite Palette – Besonders geeignet für fortgeschrittene Forschung, etwa in der Medizin, Bioinformatik und Wirtschaft. | Häufig in klinischen Studien und Gesundheitsforschung verwendet – Ideal für deskriptive und inferenzstatistische Analysen, wie zum Beispiel in der medizinischen Forschung. |
| Benutzerfreundlichkeit | Gering – Erfordert Programmierkenntnisse, was die Einstiegshürde für Anfänger erhöht. | Hoch – Einfache grafische Benutzeroberfläche, keine Programmierkenntnisse notwendig. |
| Kosten | Kostenlos – Open-Source, keine Lizenzgebühren erforderlich. | Kostenpflichtig – Hohe Lizenzgebühren, abhängig von der Version (zum Beispiel SPSS Statistics Premium). |
| Skalierbarkeit | Sehr hoch – Sehr gut geeignet für grosse Datensätze und komplexe Berechnungen, da die Programmiersprache effizient mit Daten umgehen kann. | Begrenzt – Weniger gut bei sehr grossen Datensätzen oder hochkomplexen Modellen, da die Berechnungen ressourcenintensiver sind. |
| Visualisierung | Gut – Erfordert Programmierkenntnisse, aber ermöglicht massgeschneiderte Visualisierungen (zum Beispiel ggplot2). | Sehr gut – Benutzerfreundliche, integrierte Visualisierungsfunktionen für Diagramme und Grafiken. |
Fazit: R vs. SPSS
- R bietet mehr Flexibilität und ist ideal für tiefgehende und massgeschneiderte Analysen, erfordert jedoch Programmierkenntnisse.
- SPSS eignet sich hervorragend für schnelle und benutzerfreundliche Analysen, besonders in klinischen und medizinischen Bereichen, hat jedoch Einschränkungen bei komplexeren oder fortgeschrittenen Modellen.
Spline Regression: Entwicklungen in der Medizin
Spline Regression und maschinelles Lernen
Die Kombination von Spline Regression mit Machine-Learning-Algorithmen ermöglicht eine präzisere Modellierung komplexer medizinischer Daten. Ein aktueller Anwendungsfall ist die Analyse von medizinischen Bilddaten. In der Radiologie können Spline Regressionen helfen, nichtlineare Beziehungen zwischen verschiedenen Bildmerkmalen, wie etwa der Form von Tumoren oder der Veränderung von Organen im Verlauf der Behandlung, zu modellieren. Machine-Learning-Algorithmen wie Random Forests oder Gradient Boosting können eingesetzt werden, um diese Merkmale zu klassifizieren und eine genauere Diagnose zu unterstützen.
Ein weiteres Beispiel ist die Anwendung in der Krankheitsvorhersage. In der Epidemiologie wird Spline Regression verwendet, um nichtlineare Trends in der Ausbreitung von Krankheiten wie Diabetes oder Krebs zu modellieren. Machine-Learning-Modelle helfen, diese Muster zu erkennen und individuelle Risikoprognosen zu erstellen, was eine frühzeitige Diagnose und präventive Massnahmen ermöglicht.
Spline Regression in der Zeitreihenanalyse
Die Zeitreihenanalyse mit Spline Regression spielt in der Medizin eine Schlüsselrolle bei der Modellierung von saisonalen Schwankungen und langfristigen Trends in Gesundheitsdaten.
Ein typisches Beispiel ist die Analyse von Patientenmonitoring-Daten in Intensivstationen. Die Herzfrequenz, Blutdruck oder Körpertemperatur eines Patienten folgen oft saisonalen Schwankungen, etwa im Zusammenhang mit Infektionskrankheiten oder klimatischen Bedingungen. Die Spline Regression Anwendung kann diese nichtlinearen Veränderungen besser erfassen als traditionelle Modelle und somit eine genauere Frühwarnung für gesundheitliche Verschlechterungen bieten.
Spline Regression und Big Data
In der Medizin stellt die Analyse von Big Data eine besondere Herausforderung dar, da die Menge an Daten aus verschiedenen Quellen, wie medizinischen Bilddaten, genetischen Informationen, Krankenakten und neuerdings auch Wearables, enorm ist. Hier bietet die Spline Regression eine leistungsstarke Methode, um diese umfangreichen Datensätze zu analysieren und präzise Modelle zu entwickeln.
Ein Beispiel hierzu findet sich in der medizinischen Forschung: Die Analyse von epidemiologischen Daten aus weltweit gesammelten Krankenakten ermöglicht es, gesundheitliche Risiken und Trends besser zu verstehen. In der Präzisionsmedizin wird die Spline Regression genutzt, um komplexe Zusammenhänge zwischen genetischen Prädispositionen und Umweltfaktoren zu erkennen. So können Behandlungsansätze entwickelt werden, die individuell auf den jeweiligen Patienten abgestimmt sind.
Mit der Unterstützung von Cloud-Computing und GPU-beschleunigten Algorithmen wird es möglich, die Spline Regression auf äusserst grosse Datensätze anzuwenden und in Echtzeit wertvolle klinische Einblicke zu gewinnen, beispielsweise in der Gesundheitsüberwachung oder der Verlaufskontrolle von Behandlungen.
Diese Ansätze verdeutlichen, wie Spline Regression in Verbindung mit modernen Technologien wie Machine Learning und Big Data dazu beiträgt, die medizinische Forschung und Praxis zu optimieren und Patienten eine noch präzisere Behandlung zu ermöglichen.